2025-05-02 京都大学
<関連情報>
- https://www.kyoto-u.ac.jp/ja/research-news/2025-05-02-3
- https://www.kyoto-u.ac.jp/sites/default/files/2025-05/web_2505_Wada-f9876cbcdac9633e14655be68f0b513a.pdf
- https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.162302
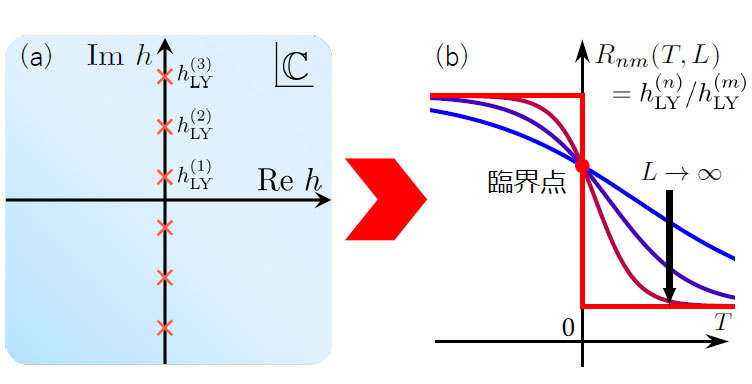
リー・ヤン・ゼロの比を用いた臨界点の特定 Locating Critical Points Using Ratios of Lee-Yang Zeros
Tatsuya Wada, Masakiyo Kitazawa, and Kazuyuki Kanaya
Physical Review Letters Published: 24 April, 2025
DOI: https://doi.org/10.1103/PhysRevLett.134.162302
Abstract
We propose a method to numerically determine the location of a critical point in general systems using the finite-size scaling of Lee-Yang zeros. This method makes use of the fact that the ratios of Lee-Yang zeros on various spatial volumes intersect at the critical point. While the method is similar to the Binder-cumulant analysis, it is advantageous in suppressing the finite-volume effects arising from the mixing of variables in general systems. We show that the method works successfully for numerically locating the critical point in the three-dimensional three-state Potts model with a nonzero external field.