2025-01-10 東京大学,九州大学
発表のポイント
- マヨネーズや泡沫などを代表例とする、柔らかい粒子が乱雑に充填された物質(ソフトジャム固体)について、その粘弾性を定量的に理解することに、世界で初めて成功しました。
- 特に、ソフトジャム固体が示す粘性の急激な増大(異常粘性損失)と、ガラスが普遍的に有する異常振動(ボゾンピーク振動)に、関係があることを発見しました。
- 本研究で発見されたソフトジャム固体とガラスの関係に基づいて、多様なアモルファス固体の統一的な理解が大きく促進されることが期待されます。
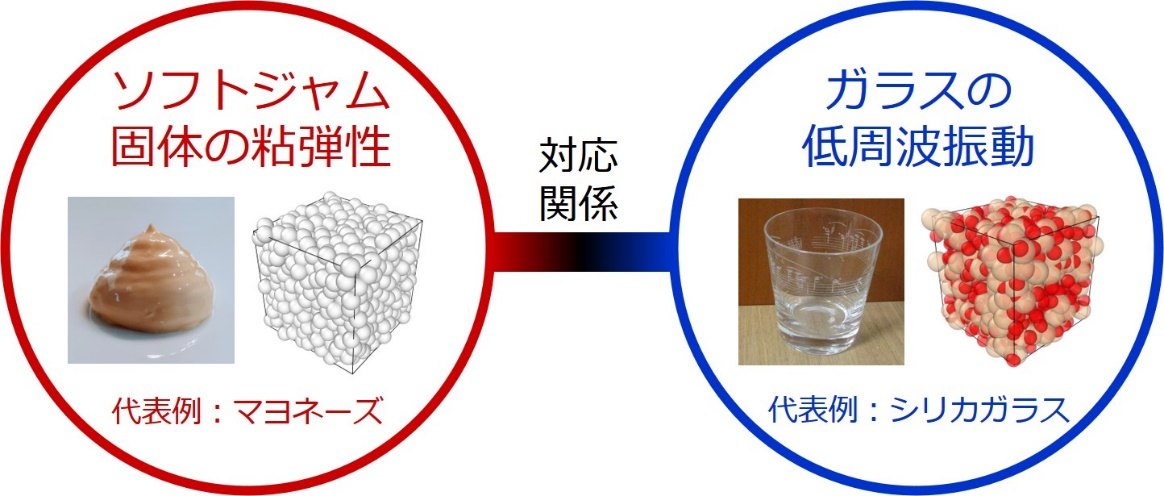
本研究の成果の概念図
概要
マヨネーズや泡沫などは、柔らかい球状粒子が乱雑に充填された物質であり、ソフトジャム固体(注1)と呼ばれます。ソフトジャム固体は、液体と固体の中間の性質である粘弾性(注2)を示しますが、その理解は十分ではありませんでした。特に、異常粘性損失(注3)と呼ばれる、遅い変形に対して粘性が急激に増大する現象について、理解が困難でした。
今回、東京大学大学院総合文化研究科の原雄介大学院生(研究当時)と池田昌司准教授は、九州大学大学院理学研究院の水野大介教授らと共同で、ソフトジャム固体の粘弾性を理解することに成功しました。典型例として、マヨネーズのような高密度エマルジョンに注目し、粘弾性の微視的理論の構築と、マイクロレオロジー実験(注4)による粘弾性測定を行ったところ、理論と実験が定量的に一致することを見出しました。
またこの理論により、ソフトジャム固体の異常粘性損失が、ガラス(注5)の異常振動と関係していることがわかりました。ガラスは、ボゾンピーク振動(注6)と呼ばれる、空間的に乱れた低周波振動を、普遍的に持つことが知られています。今回の研究で、ソフトジャム固体の異常粘性損失は、ボゾンピーク振動と同様の特性を持ち、同様の法則に従うことがわかりました。
この発見は、ソフトジャム固体の粘弾性を解明するだけでなく、ソフトジャム固体とガラスの隠れた関係を暴くものであり、多様なアモルファス固体(注7)の物性の統一的理解を大きく推進する成果と言えます。本研究成果は、日本時間1月10日19時(米国東部時間:10日午前5時)に「Nature Physics」誌に掲載されました。
発表内容
① 研究の背景
我々の身の回りには、マヨネーズや泡沫など、固体とも液体ともつかない物質がたくさんあります。上記の物質の共通点は、柔らかい球状粒子が乱れた配置のまま固化していることにあります。例えばマヨネーズは油滴が乱雑充填された物質であり(図1左)、泡沫は気泡が乱雑充填された物質です。このような物質群を「ソフトジャム固体」と呼びます。ソフトジャム固体は変形に対して粘弾性を示しますが、これまで、その定量的な理解は非常に困難でした。特に遅い変形に対して粘性が急激に増大する異常粘性損失と呼ばれる現象について、その起源が理解されていませんでした。
視野を広げてみると、自然界には、分子や原子が乱雑な配置のまま固化した物質が数多く存在し、ガラスと呼ばれています。例えばシリカガラスは、ケイ素と酸素が乱れた配置のまま動けなくなった物質です(図1右)。構造に注目すると、ソフトジャム固体とガラスは、乱雑であるという点で似通っています。では、両者の物性に共通点はあるのでしょうか?
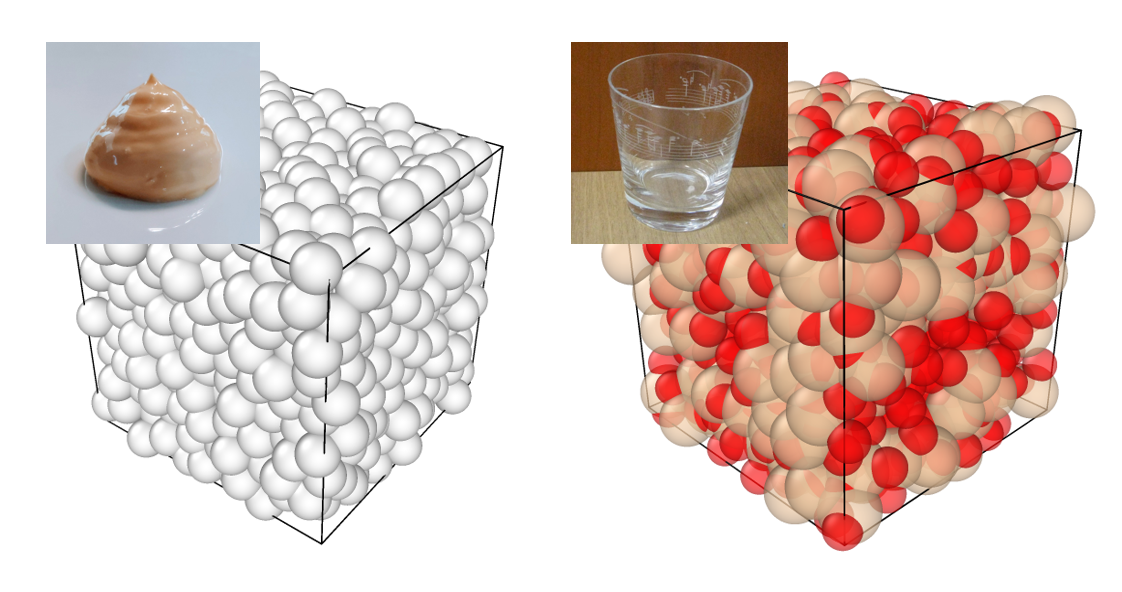
図1:エマルジョンとガラスの微視的構造
左図:エマルジョンの数理モデルのスナップショット。球は油滴を表す。インセットはエマルジョンの代表例であるマヨネーズ。右図:シリカガラスの数理モデルのスナップショット。黄球はケイ素原子、赤球は酸素原子を表す。インセットはガラスコップ。
② 研究の内容
本研究では、ソフトジャム固体の粘弾性の理解に成功しました。ソフトジャム固体の代表例として高密度エマルジョンに注目し、実験と理論で粘弾性を研究しました。実験的には、直径0.5㎛程度の油滴からなるエマルジョンを用意し、マイクロレオロジーという手法により、広帯域での粘弾性測定を実現しました。理論的には、高密度エマルジョンの数理モデルに対して、マイクロレオロジーを記述する線形応答理論を構築し、粘弾性の計算を実現しました。実験と理論を直接比較した結果、両者が定量的に一致することを見出しました(図2)。これにより、よく制御された実験系については、ソフトジャム固体の粘弾性を精密に予言できるようになりました。
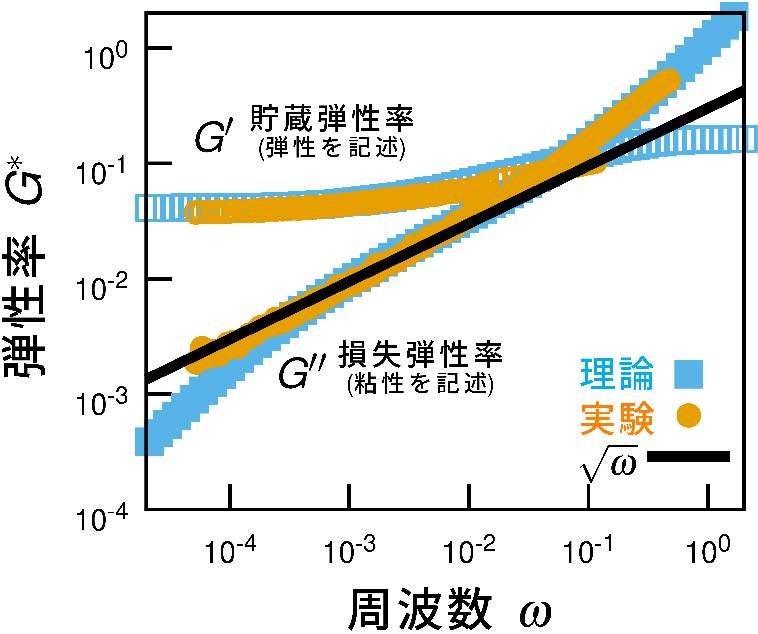
図2:高密度エマルジョンの粘弾性
縦軸が弾性率で横軸が周波数。弾性を記述する貯蔵弾性率 G’ と、粘性を記述する損失弾性率 G” の双方で、実験と理論がいい一致を示している。また実験・理論ともに、幅広い周波数領域で、異常粘性損失 G”~√ωを示している。
またこの理論から、ソフトジャム固体の異常粘性損失が、ガラスが普遍的に持つ低周波振動であるボゾンピーク振動と直接的に関係することがわかりました。ガラスの中の原子・分子の振動運動は、その構造の乱れに起因して、きれいな平面波だけでなく、空間的に乱れた振動を示すことが知られています。このような振動はボゾンピーク振動と呼ばれ、長年、ガラスの物理学の主要なテーマの一つとして研究されてきました。我々の理論によると、ソフトジャム固体の構成粒子もこのボゾンピークと酷似した低エネルギーの運動状態を示し(図3)、この運動状態が大きな粘性を生み出すことがわかりました。すなわち、ボゾンピークの理論により、異常粘性損失を説明できることがわかったのです。

図3:ソフトジャム固体における粒子の運動の様子
エマルジョンの数理モデルにおいて、異常粘性損失に寄与する粒子の運動の様子を可視化した。球は粒子、矢印は粒子の変位を表す。ガラスのボゾンピーク振動と同様に、低エネルギーでありながら、空間的に乱れた変位場が現れる。
③ 今後の期待
我々の身の回りにあるものは大抵複雑で、理論的な理解は困難です。しかし今回の結果は、エマルジョンのような身近で複雑な物質に対しても、理論と実験が精密に一致するレベルまで、我々の理解が進んでいることを示しています。自然界には、マイクロゲルから生体の細胞質や細胞集団まで、多様なソフトジャム固体が存在します。本研究のアプローチを用いることで、これらの物質の粘弾性の理解が大きく進むことが期待されます。
物理学では、ソフトジャム固体やガラスなどの構造的に乱れた固体は、ひとまとめに、アモルファス固体と呼ばれます。例えば、砂山のような粉粒体もアモルファス固体の一種です。日常経験ではガラスと砂山は全く異なるもののように思われますが、構造的に乱れているという点に注目すれば、両者は似通っているわけです。これらのアモルファス固体の物性を統一的に理解することは、物理学の大きな目標の一つとなっています。本研究の成果は、この方向での一里塚であり、多様なアモルファス固体の物性の統一的理解を大きく推進する成果と言えます。
発表者・研究者等情報
東京大学 大学院総合文化研究科 広域科学専攻
原 雄介 博士課程(研究当時)
池田 昌司 准教授
九州大学 大学院理学研究院 物理学部門
松岡 亮佑 修士課程(研究当時)
江端 宏之 助教
水野 大介 教授
論文情報
雑誌名:Nature Physics
題名:A link between anomalous viscous loss and the boson peak in soft jammed solids
著者名:Yusuke Hara*, Ryosuke Matsuoka, Hiroyuki Ebata, Daisuke Mizuno, Atsushi Ikeda
DOI:10.1038/s41567-024-02722-7
URL:https://www.nature.com/articles/s41567-024-02722-7
研究助成
本研究は、科研費 特別研究員奨励費(23KJ0368)、基盤研究B(20H01868、21H01048)、基盤研究A(20H00128、24H00192)、新学術領域研究(22H04848)、基盤研究C(22K03552)、及びホソカワ粉体工学振興財団(HPTF21509)、JST 次世代研究者挑戦的研究プログラム(JPMJSP2108)、JST CREST(JPMJCR24T2)、JST ERATO(JPMJER2401)、日本学術振興会 先端研究拠点事業(JPJSCCA20230002)による支援を受けたものです。
用語説明
(注1)ソフトジャム固体
柔らかい粒子が乱雑な構造のまま固化した物質群を、ソフトジャム固体と呼びます。ソフトジャム固体のうち、マヨネーズなどのエマルジョンは、油滴粒子が水中に分散して乱雑充填した物質であり、泡立てたシャンプーのような泡沫は、気泡粒子が水中に分散して乱雑充填した物質です。構成粒子の充填率が64% 程度を超えると、粒子がランダム最密充填状態に陥り、乱雑な配置のまま固化します。
(注2)粘弾性
物質を変形させるには力を要しますが、変形の大きさに比例する力を弾性、変形速度に比例する力を粘性と呼びます。物質の粘弾性を調べるには、物質に周波数ωの振動的な変形を加え、応力を測定し、変形の大きさに比例する成分である貯蔵弾性率 G'(ω) と、変形速度に比例する成分である損失弾性率 G”(ω) を決定します。標準的な粘弾性モデルであるフォークト模型では、弾性係数をE、粘性係数をηとして、G'(ω)=E,G”(ω)=ηωとなります。
(注3)異常粘性損失
ソフトジャム固体では、幅広い周波数領域でG'(ω)=E,G”(ω)~√ω が成立することが知られています。これを異常粘性損失と呼びます。これは、損失弾性率 G”(ω) が周波数ωに比例するフォークト模型とは大きく異なる挙動であり、実効的な粘性が G”(ω)/ ω~1/√ω のように、低周波で異常に大きくなることを意味しています。
(注4)マイクロレオロジー実験
通常の粘弾性測定では、物質に巨視的な変形をかけて、巨視的な応力を観察します。一方でマイクロレオロジーという手法では、物質中にマイクロメーターサイズのコロイド粒子を挿入し、そのコロイド粒子の運動をレーザーで追跡することで、物質の粘弾性を測定します。マイクロレオロジーは、通常の粘弾性測定が不可能なサンプルに適用できることや、高周波数領域の測定が可能な事が特徴です。
(注5)ガラス
ガラスは幅広い用語で、文脈により、様々な意味で用いられます。しかし本稿では、原子・分子が乱雑な構造のまま固化した固体をガラスと呼びます。シリカガラスは、ケイ素原子と酸素原子が乱れた配置のまま固化した物質です。その他にも、高分子が乱れた配置のまま固化した高分子ガラスや、金属原子が乱れた配置のまま固化した物質である金属ガラスなどがあります。
(注6)ボゾンピーク振動
固体中の振動は、多くの場合、三角関数で表される平面波となります。すなわち、振動は空間的に周期構造を持ちます。しかしガラスの場合は、空間的に乱れた振動が、低周波数領域にすら存在することが知られており、この振動はボゾンピーク振動と呼ばれています。ボゾンピーク振動は、ガラスの物理で長く研究されてきており、その理解が深まっています。
(注7)アモルファス固体
構成要素が乱れた配置のまま固化した物質を総称して、アモルファス固体と呼びます。ソフトジャム固体やガラスは、アモルファス固体の一例です。その他には、砂山や穀物など、ミリメーターやセンチメーター程度のサイズの粒からなる粉粒体もその一例と言えます。