2024-11-07 東京大学
発表のポイント
- 無機結晶化学の知見を数理計画問題として定式化した結晶構造探索手法を考案し、銅酸化物超伝導体La2-xSrxCuO4の結晶構造などさまざまな酸化物の結晶構造を再現した。
- 従来手法とは比較にならないほど非常に小さい計算コストでの網羅探索が可能となり、無機結晶化学の知見に適合する未知の結晶構造プロトタイプの発見が可能であることを示した。
- 同手法の応用により、高機能材料として有用なカルコゲン化物や複合アニオン化合物の予測と発見への貢献が期待される。
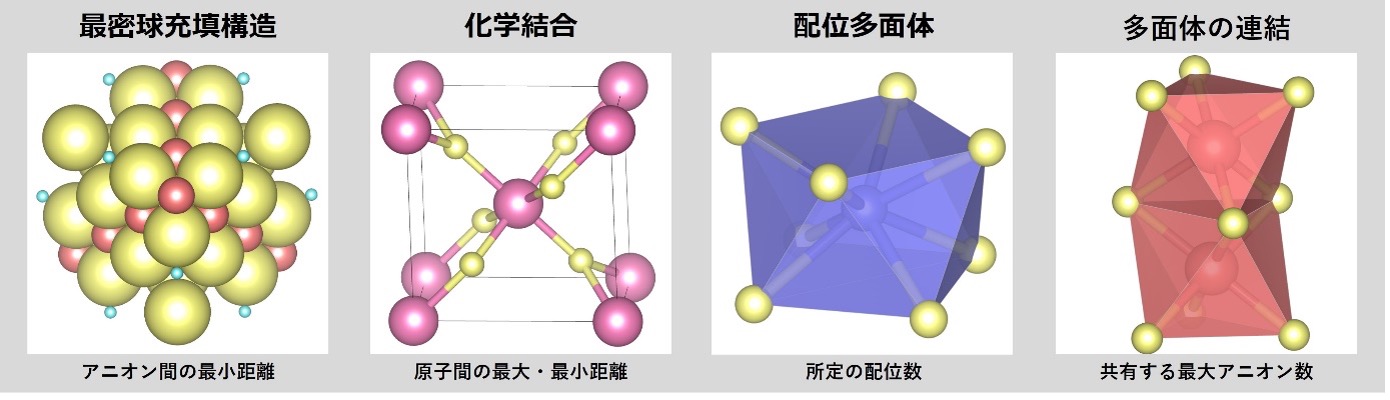
数理計画問題の最適解として結晶構造を再現するための等式・不等式拘束条件
概要
東京大学物性研究所の小正路 崚太郎 大学院生(当時)と尾崎 泰助 教授の研究グループは、無機結晶化学の経験則を数理計画問題として定式化した結晶構造探索手法「数理結晶化学」を考案し、酸化物の結晶構造プロトタイプを網羅的に探索する新しいアルゴリズムを開発しました。このアルゴリズムにより、酸化物の結晶構造を包括的に理解する手段を提供するとともに、将来的には第一原理計算(注1)と組み合わせて新物質の計算による予測が可能になると期待されます。
固体中の原子は三次元空間に規則正しく配置されていますが、最も安定な結晶構造を計算により予測するのは一般に困難です。無機結晶化学は結晶構造の構成原理を経験的知見から体系的に説明するものの、ポーリング則(注2)と呼ばれる五つの規則を同時に満たす結晶構造は例外的であることが知られています。研究グループは、現代的な視点から無機結晶化学を再検討し、膨大な選択肢の中から非常に小さな計算コストで実現可能な結晶構造を「最適解」として特定する数理計画法を開発しました。複雑な酸化物の候補構造を、無数の選択肢から数千通りまで絞り込むことができれば、第一原理計算を用いて最安定構造を予測することが可能になります。これにより同手法をスクリーニングに用いた、計算による新物質の発見につながることが期待されます。
この研究成果は、米国科学誌「Physical Review Materials」に2024年11月6日(現地時間)に掲載されました。
発表内容
研究の背景
無機固体の多くは原子が周期的に配置した結晶構造から構成されており、三次元の繰り返し単位である単位格子(注3)には数個から数十個の原子が含まれています。固体の性質は構成する原子の価電子状態により決定されますが、組成が同じでも結晶構造が変わると性質は大きく変化します。そのため、結晶構造は物質デザインの出発点となりますが、実験的に合成できる結晶構造を予測することは簡単ではありません。これは、単位格子の形状に任意性があるだけでなく、単位格子内の原子配置にも膨大な自由度があり、この問題がNP困難な最適化問題(注4)に分類されるからです。例えば、4×4×4の格子点から2つの点を選ぶ自由度は2,016通りですが、4つの点を選ぶ自由度は645,376通りです。最も安定な構造を予測する場合、本質的には全ての可能性におけるエネルギーを評価する必要がありますが、単位格子中の原子が増えると爆発的に原子配置の自由度が増えるため、最安定構造の決定が困難になります。そのため、近年は、進化型アルゴリズムや粒子群最適化法などの最適化法に基づく結晶構造探索アルゴリズムが開発され、100 GPaを超える超高圧下での超伝導水素化物の予測などで成功を収めています。これらは複数の初期構造を生成して同時に最適化を進めながら最安定構造を推定する発見的手法です。未知の結晶構造を発見できる可能性を秘めていますが、最安定構造は必ずしも発見できず、予測した構造の安定性を俯瞰的観点から説明できるとは限りません。
一方で、無機結晶化学は結晶構造の構成原理を定性的に説明します。結晶化学では、化学結合の特性に応じた原子半径を経験的に定めますが、原子球をできるだけ密に詰めた結晶構造を構成しようとすることが知られています。例えば、多くの単体金属が構成するFCC構造やHCP構造(注5)などの結晶構造は、剛体球を最も隙間なく詰めた最密球充填構造に対応しており、最密ではない金属間化合物においても球充填構造としての側面を強く持っています。酸化物の結晶構造においても、酸素イオンがFCC構造などの最密球充填構造を構成し、その隙間に小さな金属イオンが配置された結晶構造が多くみられます。また、イオン結合性結晶は配位多面体(注6)の連結体としての側面を持ち、結晶構造の構成要素となる主な配位多面体の種類や、中心に配置されたカチオン(注7)の電荷の大きさに応じた多面体の連結傾向などが経験的に知られています。これらの知見はモデルポテンシャルの構築の際に利用されているものの、直接的に計算による結晶構造予測へ組み込む方法論は確立されていませんでした。
研究の内容
従来の結晶構造探索手法では、一般に結晶構造のエネルギーは第一原理計算により評価されますが、計算コストが大きいことから、試行できる構造数が制限されています。研究グループは、酸化物の結晶構造に着目し、従来手法とは比較にならないほど非常に小さな計算コストで結晶構造プロトタイプを網羅探索できる数学的枠組みを考案しました。本手法では結晶構造探査を数理計画問題として定式化します。配位数とイオン間の距離に対する等式及び不等式条件のセットを構成し、これらの拘束条件式の全てを満たす原子配置を数理計画法により探索します。
まず、無機結晶化学が体系化する結晶構造の構成原理を再現できる拘束条件を導入しました。酸化物イオンは剛体球としての側面を強く持つことから、イオン半径の和より近くなることはできないという剛体球的な拘束条件を導入します。また、電子は物質中に波として存在していることから明確に化学結合を定義することは難しい問題ですが、本研究では、原子間距離が定められた範囲内に収まらなければならないという不等式条件として化学結合を定義します。ランダムに生成した初期構造を結晶構造プロトタイプまで最適化させるため、他にも三種類の拘束条件を導入しています。
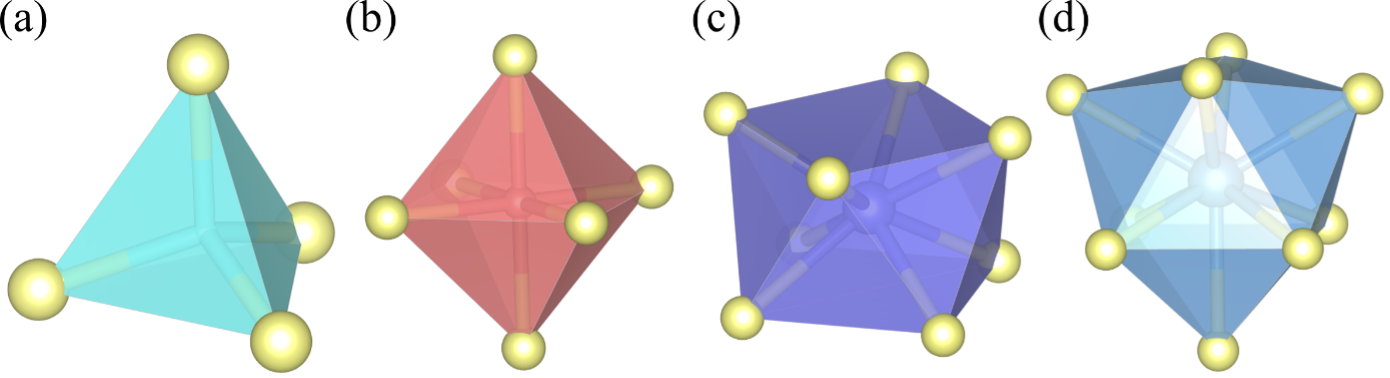
図1:カチオンのサイズと配位多面体
n個の酸素イオンと接することが可能な最小カチオンが構成する配位多面体。カチオンのサイズが大きくなるほど配位数が増加する。(a)正四面体。(b)正八面体。(c)反四角柱。(d)四角面三冠三角柱。
次に、構造プロトタイプを構成するモデルカチオンを定義しました。電子の波動性により原子の大きさを明確に定義することは困難ですが、無機結晶化学では経験的知見から化学結合の種類に応じた原子半径を定義しています。イオン結合性結晶においては、カチオンの種類が変わっても同じ構造で安定になることがありますが、これはカチオンの大きさがほぼ同一であることが理由の一つであり、無機結晶化学ではカチオンとアニオン(注7)の原子半径の比が配位多面体の種類を決定すると説明します。カチオンが大きくなるほど多くの酸素イオンから成る配位多面体を構成しますが、これは酸素イオン間を剛体球と見なしたときに、カチオンは可能な限り多くの酸素イオンと接することができる配位多面体を選択していることを意味します。そこで、n個の酸素イオンと配位多面体を構成できる最小半径を用いてモデルカチオンの大きさを定義しました(図1)。ただし、大きなカチオンほど化学結合距離に柔軟性を持ち始め、柔らかい球のようになるため、その柔軟性を最大・最小イオン半径を定義して再現しました。また、大きなカチオンでも少ない配位数を取る場合もあるので、所定の配位数という拘束条件を導入することが重要であることが分かりました。これらの等式および不等式条件は、原子あたりおよそ50となり、系全体では多くの条件が課されます。本手法ではこれらの全ての条件を満たす単位格子の形状と原子配置を見つける数理計画問題として、結晶構造探査を捉え直します。
イオン結合性結晶や金属間化合物を含め、多くの結晶構造において最密充填原理は主要な構成原理の一つです。そこで、全てのモデルカチオンが所定の配位数の条件を満たし、全ての原子間距離の最大・最小距離の不等式条件を満たしながら単位格子の体積を最小化したものを結晶構造プロトタイプと定義しました。ただし、ランダムに生成したほとんどの初期構造は全ての条件を満たすことができないため、原子間距離の拘束条件下での単位格子の最小化問題(構造最適化問題)と、所定の条件下で化学結合数を最大化する問題に切り分けて、交互に最適化を進めることで最適解への変化を促すアルゴリズムを考案しました。構造最適化問題を解く際には、一般に不等式条件は二階微分可能な滑らかな関数を用いますが、線形ポテンシャルに近似することで非常に小さな計算コストで最適解へ収束できることが分かりました。
開発したアルゴリズムを用いて結晶構造プロトタイプの網羅探索を実行した結果、さまざまな種類の配位多面体から成る結晶構造を再現できました。また、ランダムな初期構造から構造探査をすると、第一原理計算によるエネルギー評価では膨大な数の最安定ではない構造が得られますが、提案する数理計画問題ではその数が激減することが分かりました。例えば、酸素イオンO2-と同じ大きさのカチオンAと八面体配位を構成するカチオンBをA4B4O12として混ぜてみると僅か4つの最適解が見つかり、その全てがペロブスカイト構造などの実験的に知られた結晶構造に対応していました。他にも、銅酸化物超伝導体のLa2-xSrxCuO4、スピングラスなどの量子物性を示すα-Pyrochlore構造、透明電極材料IGZOなどのさまざまな配位多面体からなる結晶構造の再現に成功しました(図2)。特に銅酸化物超伝導体のLa2-xSrxCuO4に関しては、本組成比に対する結晶構造の唯一解である可能性を示唆しています。組成比に応じて、複数の最適解が見つかる場合もあれば、唯一の解しか存在しない場合もあり、組成比と結晶構造の多形性の間に多面体の空間充填問題と密接な関係がある数学的な構造が存在すると考えられます。また、実験的に知られていない構造も最適解として網羅的に発見できるため、その中に未発見の結晶構造が眠っている可能性があると考えています。考案した数理計画問題をさらに洗練・拡張することで、酸化物に限らず、カルコゲン化物や複合アニオン化合物の結晶構造を最適解として体系化することで、未知の結晶構造の予測に繋がることが期待されます。
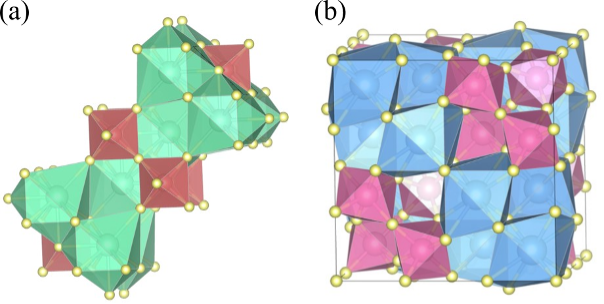
図2:結晶構造に対応する最適解の例
最大・最小イオン半径や配位数で定義したモデルカチオンをさまざまな組成で混合し、最適解を網羅探索すると、実験的に知られた結晶構造が再現できる。(a)銅酸化物超伝導体La2-xSrxCuO4の結晶構造。(b)スピングラスなどの量子物性を示すα-Pyrochlore構造。
今後の展望
無機結晶化学は結晶構造の構成原理を定性的に説明し、実験による新物質探索の出発点となっていますが、計算による物質探索への有効な利用法は確立されていません。1929年にポーリングによりまとめられたイオン結合性結晶構造を構成する五つの規則は結晶構造を理解する基礎となったものの、全ての規則を満たす結晶構造は少数であることも知られています。本研究の成果は、計算機が発達した現代的視点から無機結晶化学を再考することで、結晶構造プロトタイプを計算により網羅探索できるような数学的枠組みが構築できることを示唆しています。従来の手法がエネルギー曲面を効率的に探索する手法であったのに対して、提案手法では無機結晶化学で集約された幾何学的知見を等式及び不等式条件に変換し、結晶構造探査を数理計画問題として捉えなおす新しい方向性を示しています。組成に応じて複数の多形が生じる理由も本手法が答えを与える可能性があり、ポーリング則を越えて精緻にかつ包括的に酸化物の結晶構造を理解する手段となるかも知れません。数理計画問題に基づく結晶化学、略して「数理結晶化学」という新学術領域の開拓が期待されます。
開発した手法はより有用な物質の探索へ応用が見込まれます。酸化物やカルコゲン化物は、現代技術の至る所で利用される重要な物質群です。近年は、複数種類のアニオンを混ぜることで機能を改善した複合アニオン化合物という物質群も注目されています。蓄電材料をはじめとする、グリーントランスフォーメーション(GX)の実現に不可欠な高機能材料も、これらの物質群に含まれている可能性が高いと考えられます。結晶構造の構造特性に違いはあるものの、配位多面体の連結体であることやアニオンが剛体球としての側面を強く持つなど、基本的な構成原理は共通しています。本研究の枠組みをこれらの物質群まで拡張し、結晶構造プロトタイプを網羅的に探索することで、材料探索からデバイスへの応用までの研究プロセスを加速できると考えています。
発表者・研究者等情報
東京大学
物性研究所
小正路 崚太郎 研究当時:大学院生 (大学院理学系研究科物理学専攻)
現:産業技術総合研究所 研究員
尾崎 泰助 教授
論文情報
雑誌名 : Physical Review Materials
題名 : Mathematical crystal chemistry: A mathematical programming approach to crystal structures of inorganic compound
著者名 : Ryotaro Koshoji* and Taisuke Ozaki
DOI:10.1103/PhysRevMaterials.8.113801
用語解説
- (注1)第一原理計算 :
- 量子力学の基礎方程式から出発して計算により物性値を計算する方法のこと。主に密度汎関数理論に基づく手法が用いられる。限りなく正確なシミュレーションが可能だが、物質を構成する原子が増えるにつれて、計算コストが増大する。
- (注2)ポーリング則 :
- イオン結合性結晶の五つの重要な構成原理のこと。カチオン周りに配位多面体が構成されることや、カチオン電荷が大きくなると二つの配位多面体は面共有をしなくなるなど、結晶構造を考察する指針を与えている。
- (注3)単位格子 :
- 結晶構造とは周期的な原子の空間配置のことである。繰り返し単位を三次元上に規則正しく並べることで結晶構造が再構成できるが、その繰り返し単位を単位格子と呼ぶ。
- (注4)NP困難な最適化問題 :
- 組み合わせや自由度が膨大なため、大きな系ではノイマン型コンピューター(現在存在する一般的なほとんどのコンピューター)で最適解を求めることが実質的に不可能な問題のこと。巡回セールスマン問題などが有名である。
- (注5)FCC構造・HCP構造 :
- 三角格子を基に大きさが等しい球を並べ、互いに接している3つの球の中心に4つ目の球を置くように層を重ねていくと、最も隙間の少ない最密球充填構造が構成できることが知られている。層の重ね方には自由度があるため、FCC(面心立方格子)構造やHCP(六方最密充填)構造など、充填率の等しいさまざまな構造が構成できる。
- (注6)配位多面体 :
- 原子が複数の原子と化学結合を構成するとき、隣接する配位した原子間を結ぶと、ある程度の対称性を持った多面体を構成することが多く、それを配位多面体と呼ぶ。
- (注7)カチオン・アニオン :
- 原子は、正の電荷を持つ原子核と、負の電荷を持つ電子から構成されている。化合物が形成される際、原子が電子を失ったり受け取ったりすることで電荷を帯びる。電子を失って正の電荷を持つようになった原子や分子をカチオン(陽イオン)、電子を受け取って負の電荷を持つようになった原子や分子をアニオン(陰イオン)と呼ぶ。