2024-04-12 東京大学
発表のポイント
◆ これまで線形系に限定されてきた二次元物質のトポロジカル指数を非線形系に拡張し、バルク・エッジ対応と呼ばれるトポロジカル物質の基本原理が非線形系でも成立することを示した。
◆ とくに非線形性の強さによって、物質の状態を表す数学的性質(トポロジー)が変化するという、非線形系に固有の非線形トポロジカル相転移の存在を明らかにした。
◆ 非線形性を活用した柔軟な制御性とノイズに対する頑健性を併せ持つデバイスの設計原理につながることが期待される。
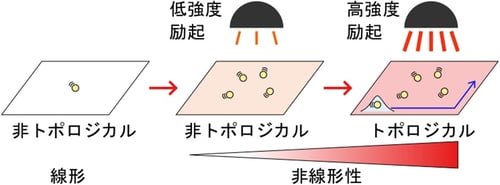
非線形性によって誘起されるトポロジカル相転移。波の媒質である黄色の粒子が多数集まることにより生じる非線形効果によってトポロジーの変化が実現する。
概要
東京大学大学院工学系研究科物理工学専攻の曽根和樹大学院生(研究当時)、江澤雅彦講師、吉岡信行助教、沙川貴大教授、および同大学大学院理学系研究科物理学専攻の蘆田祐人准教授らによる研究グループは、二次元的な非線形(注1)物質において新たなトポロジカル指数(注2)を導入し、それが試料端に局在するエッジ状態(注3)と対応するというバルク・エッジ対応(注4)が成り立つことを理論的に示しました。さらに非線形系に特有な現象として、非線形性の強さに依存してトポロジカル相が変化する相転移の存在を明らかにし、それが今回導入したトポロジカル指数で予言できることを示しました。従来のトポロジカル物質(注5)の研究はほとんどが線形系に限定されていたのに対して、本研究はそれを非線形系へと拡張する大きな一歩であると言えます。さらに今後、トポロジーの効果によるノイズに対する頑健性(注6)と、非線形性の効果による柔軟性を併せ持ったデバイスなどの開発につながることが期待されます。
発表内容
【研究背景】
近年、量子ホール系やトポロジカル絶縁体に代表される、トポロジカル物質が注目を集めています。トポロジカル物質はその試料の端にエッジ状態を持ち、不純物に邪魔をされない電流を生み出すことが知られています。エッジ状態は、連続変形で変わらないトポロジーの性質を反映するため、外界からのノイズの影響を受けにくい低消費電力デバイスなどへの応用が期待されています。このようなエッジ状態と、物質のバルク(注7)で定義されるトポロジカル指数との対応はバルク・エッジ対応と呼ばれ、トポロジカル物質の基本原理として知られています。しかし、従来のトポロジカル物質の研究のほとんどは、重ね合わせの原理(注8)が成立する線形系に限定されていました。
一方で、物理学においては非線形系も重要な役割を果たします。蛍の発光の同期現象や電気回路のような身近なものから、ナノスケールで精密に設計された光学系、さらには極低温の冷却原子(注9)まで、多くの非線形系が知られています。このような非線形系においては重ね合わせの原理が成立しないため、従来のトポロジカル物質の議論は適用できません。そのため、トポロジカル指数をどのように定義すべきか、バルク・エッジ対応は成立するのか、そもそもトポロジーの概念を適用可能か、といった基本的な問題が非線形系においては未解明のままでした。
【研究内容】
本研究では、二次元の非線形系について上記の問題を解決し、非線形トポロジカル物理の基本原理を明らかにしました。まず、線形の場合に知られていた二次元物質のトポロジカル指数を、非線形系に対して拡張しました。そして、それが非線形系のエッジ状態の数と対応していることを示し、非線形系においてもバルク・エッジ対応が成立することを明らかにしました(図1)。
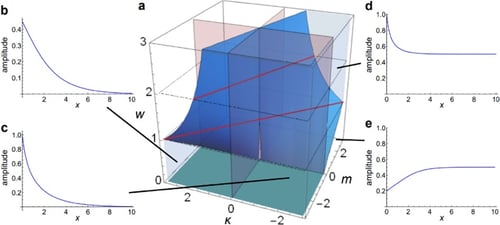
図1:非線形系のトポロジカルな相図と、対応するエッジ状態
中央の立体図aは本研究で解析された非線形系のトポロジカルな相図を表し、青の曲面が相境界となっています。図b、c、d、eの青線はそれぞれの相で得られる状態の空間分布を示しており、横軸が空間方向、縦軸が各位置での分布の大きさを表しています。青の曲面の相境界よりも手前の領域では、b、c、dのような局在したトポロジカルなエッジ状態が得られており、これらと非線形トポロジカル指数が対応することが示されます。もう一方の領域では、eに示されるような反局在する状態が現れますが、これは連続変形で消せるためトポロジカルではありません。
その際の鍵となったのは、トポロジカル指数に非線形性の強さの情報を入れることと、非線形エッジ状態のトポロジーを適切に定義することでした。その結果として、今回導入したトポロジカル指数から、非線形系に固有のトポロジカル相の存在も予言できることが示されました。とくに、非線形性の強さによってトポロジカル相が変わるという、非線形性に特有のトポロジカル現象の存在が明らかになりました。このようなトポロジカル相転移の存在は、厳密に解ける理論モデルによって明確に示すことができます。さらに、実際の実験に即した状況においても、試料端の状態の振る舞いをトポロジカル指数によって予言できることを数値シミュレーションによって明らかにしました。
【研究の意義、今後の展望】
本研究結果は、これまではほとんどが線形系に限定されてきたトポロジカル物質の理論を、非線形系へと拡張するという物理学の基本原理の観点からの意義があります。さらに、トポロジーの効果によるノイズに対する頑健性と、非線形性の効果による柔軟性を併せ持つ、新たなデバイスの設計原理へとつながることが期待されます。
発表者・研究者等情報
東京大学
大学院工学系研究科 物理工学専攻
曽根 和樹 博士課程:研究当時
江澤 雅彦 講師
吉岡 信行 助教
沙川 貴大 教授
兼:附属量子相エレクトロニクス研究センター
大学院理学系研究科 物理学専攻
蘆田 祐人 准教授
兼:知の物理学研究センター
論文情報
雑誌名:Nature Physics
題 名:Nonlinearity-induced topological phase transition characterized by the nonlinear Chern number
著者名:Kazuki Sone*, Motohiko Ezawa, Yuto Ashida, Nobuyuki Yoshioka, Takahiro Sagawa
DOI:10.1038/s41567-024-02451-x
URL:https://www.nature.com/articles/s41567-024-02451-x
研究助成
本研究は、JST ERATO「沙川情報エネルギー変換プロジェクト」(課題番号:JPMJER2302)、JST ERATO 特定領域調査「情報エネルギー変換」(課題番号:JPMJER2204)、JSPS 科学研究費助成事業新学術領域(研究領域提案型)「情報物理学でひもとく生命の秩序と設計原理」の計画研究班「情報熱力学による生体情報処理の理論研究」(課題番号:JP19H05796)、JST CREST「電気回路によるトポロジカル量子計算方法の創生」(課題番号:JPMJCR20T2)、JSPS 科学研究費助成事業基盤研究(A)「トポロジカルMEMS工学の創生」(課題番号:JP23H00171)、JST 創発的研究支援事業「量子多体物理と量子光学の融合で探る強結合開放系の物理」(課題番号:JPMJFR222U)、JSPS 科学研究費助成事業研究活動スタート支援(課題番号:JP19K23424)、JSTさきがけ研究「量子並列回路を用いた計算基盤の構築」(課題番号:JPMJPR2119)、JST 共創の場形成支援プログラム「量子ソフトウェアとHPC・シミュレーション技術の共創によるサスティナブルAI研究拠点」(課題番号:JPMJPF2221)、JST CREST「非古典スピン集積システム」(課題番号:JPMJCR20C1)、JSPS 科学研究費助成事業若手研究(課題番号:JP21K13859)、東京大学統合物質・情報国際卓越大学院(MERIT-WINGS)、東京大学Beyond AI研究推進機構の支援により実施されました。
用語解説
(注1)線形、非線形
状態変数に比例するような項のみを持つ方程式で記述される物質やシステムを線形系と呼びます。線形系では重ね合わせの原理が成り立ちます。線形な方程式の例としては、量子力学におけるシュレディンガー方程式などが挙げられます。一方で、線形な方程式で記述されないシステムを非線形系と呼びます。
(注2)トポロジカル指数
図形を連続変形したときに、不変に保たれる特徴量を指します。たとえば、ドーナツの穴の数はトポロジカル指数の一種です。これはトポロジー(位相幾何学)と呼ばれる数学の分野で研究されてきました。とくに二次元の場合は、チャーン数と呼ばれるトポロジカル指数が重要で、物理学においても量子ホール効果を記述するのに用いられてきました。今回の研究で扱っているのもこのチャーン数です。
(注3)エッジ状態
トポロジカル物質は、試料の端に特殊な状態が現れます。これをエッジ状態と呼びます。これは、ノイズや不純物に対して頑健で、散乱することなく端を伝う流れを生むという特徴が知られています。さらに、近年の研究では光学系や流体などでも同様のエッジ状態が存在することが明らかとなってきました。
(注4)バルク・エッジ対応
トポロジカル物質のバルク(注7)を特徴づけるトポロジカル指数と、その試料端に局在するエッジ状態の数が、1対1に対応するという原理がバルク・エッジ対応です。線形系の場合はこの対応が確立しており、トポロジカル物質における中心原理となっています。今回の研究では、これを非線形系へと拡張しました。
(注5)トポロジカル物質
バルクを特徴づけるトポロジカル指数が非ゼロとなるような物質群をトポロジカル物質と呼びます。トポロジカル物質は特有のエッジ状態を持ち、そのエッジ状態から期待される散乱の無い表面流などの性質を利用した低散逸デバイスへの応用が期待されています。
(注6)頑健性
トポロジカル物質のエッジ状態はノイズや不純物の影響を受けずに安定に存在できます。このようなエッジ状態の安定な性質は応用上の利点としてトポロジカル物質が注目を集める理由の1つとなっています。
(注7)バルク
物質内部の領域をバルクと呼びます。通常の物質はバルクに原子がおおむね周期的に並んでおり、その周期性を反映したバルク状態に由来する特性を示します。一方で、トポロジカル物質で見られるエッジ状態は、試料端(エッジ)において現れます。
(注8)重ね合わせの原理
線形な方程式で記述される波は、2つの波の和が再び同じ方程式の解となるという性質を持ちます。このような性質を重ね合わせの原理と呼び、線形系が非線形系よりも数学的解析が容易である大きな要因となっています。
(注9)冷却原子
原子集団をレーザーを用いて真空中で捕捉し、量子的な領域まで冷却することができます。これを冷却原子といいます。原子集団を記述する波動関数に平均場近似と呼ばれる近似を行うことにより、非線形系として記述することができます。
プレスリリース本文:PDFファイル
Nature Physics:https://www.nature.com/articles/s41567-024-02451-x