2024-08-27 アルゴンヌ国立研究所(ANL)
<関連情報>
- https://cs.uchicago.edu/news/new-classical-algorithm-enhances-understanding-of-quantum-computings-future/
- https://www.nature.com/articles/s41567-024-02535-8
- https://www.nature.com/articles/s41567-023-02308-9
- https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.131.010401
- https://www.science.org/doi/10.1126/sciadv.abi7894
- https://ieeexplore.ieee.org/document/9719705
- https://journals.aps.org/pra/abstract/10.1103/PhysRevA.104.022407
実験的ガウス粒子サンプリングをシミュレートする古典的アルゴリズム Classical algorithm for simulating experimental Gaussian boson sampling
Changhun Oh,Minzhao Liu,Yuri Alexeev,Bill Fefferman & Liang Jiang
Nature physics Published:25 June 2024
DOI:https://doi.org/10.1038/s41567-024-02535-8
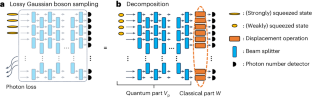
Abstract
Gaussian boson sampling is a form of non-universal quantum computing that has been considered a promising candidate for showing experimental quantum advantage. While there is evidence that noiseless Gaussian boson sampling is hard to efficiently simulate using a classical computer, current Gaussian boson sampling experiments inevitably suffer from high photon loss rates and other noise sources. Nevertheless, they are currently claimed to be hard to classically simulate. Here we present a classical tensor-network algorithm that simulates Gaussian boson sampling and whose complexity can be significantly reduced when the photon loss rate is high. Our algorithm enables us to simulate the largest-scale Gaussian boson sampling experiment so far using relatively modest computational resources. We exhibit evidence that our classical sampler can simulate the ideal distribution better than the experiment can, which calls into question the claims of experimental quantum advantage.
分子振動スペクトルのための量子に触発された古典アルゴリズム Quantum-inspired classical algorithms for molecular vibronic spectra
Changhun Oh,Youngrong Lim,Yat Wong,Bill Fefferman & Liang Jiang
Nature Physics Published:10 January 2024
DOI:https://doi.org/10.1038/s41567-023-02308-9

Abstract
Plausible claims for quantum advantage have been made using sampling problems such as random circuit sampling in superconducting qubit devices, and Gaussian boson sampling in quantum optics experiments. Now, the major next step is to channel the potential quantum advantage to solve practical applications rather than proof-of-principle experiments. It has recently been proposed that a Gaussian boson sampler can efficiently generate molecular vibronic spectra, which are an important tool for analysing chemical components and studying molecular structures. The best-known classical algorithm for calculating the molecular spectra scales super-exponentially in the system size. Therefore, an efficient quantum algorithm could represent a computational advantage. However, here we propose an efficient quantum-inspired classical algorithm for molecular vibronic spectra with harmonic potentials. Using our method, the zero-temperature molecular vibronic spectra problems that correspond to Gaussian boson sampling can be exactly solved. Consequently, we demonstrate that those problems are not candidates for quantum advantage. We then provide a more general molecular vibronic spectra problem, which is also chemically well motivated, for which our method does not work and so might be able to take advantage of a boson sampler.
ボソンサンプリングにおけるクロスエントロピー測定の偽装 Spoofing Cross-Entropy Measure in Boson Sampling
Changhun Oh, Liang Jiang, and Bill Fefferman
Physical Review Letters Published 6 July 2023
DOI:https://doi.org/10.1103/PhysRevLett.131.010401
Abstract
Cross-entropy (XE) measure is a widely used benchmark to demonstrate quantum computational advantage from sampling problems, such as random circuit sampling using superconducting qubits and boson sampling (BS). We present a heuristic classical algorithm that attains a better XE than the current BS experiments in a verifiable regime and is likely to attain a better XE score than the near-future BS experiments in a reasonable running time. The key idea behind the algorithm is that there exist distributions that correlate with the ideal BS probability distribution and that can be efficiently computed. The correlation and the computability of the distribution enable us to postselect heavy outcomes of the ideal probability distribution without computing the ideal probability, which essentially leads to a large XE. Our method scores a better XE than the recent Gaussian BS experiments when implemented at intermediate, verifiable system sizes. Much like current state-of-the-art experiments, we cannot verify that our spoofer works for quantum-advantage-size systems. However, we demonstrate that our approach works for much larger system sizes in fermion sampling, where we can efficiently compute output probabilities. Finally, we provide analytic evidence that the classical algorithm is likely to spoof noisy BS efficiently.
高次元ガウシアンボソンサンプリングによる量子計算の優位性 Quantum computational advantage via high-dimensional Gaussian boson sampling
Abhinav Deshpande, Arthur Mehta, Trevor Vincent, Nicolás Quesada, […], and Ish Dhand
Science Advances Published:5 Jan 2022
DOI:https://doi.org/10.1126/sciadv.abi7894

Abstract
Photonics is a promising platform for demonstrating a quantum computational advantage (QCA) by outperforming the most powerful classical supercomputers on a well-defined computational task. Despite this promise, existing proposals and demonstrations face challenges. Experimentally, current implementations of Gaussian boson sampling (GBS) lack programmability or have prohibitive loss rates. Theoretically, there is a comparative lack of rigorous evidence for the classical hardness of GBS. In this work, we make progress in improving both the theoretical evidence and experimental prospects. We provide evidence for the hardness of GBS, comparable to the strongest theoretical proposals for QCA. We also propose a QCA architecture we call high-dimensional GBS, which is programmable and can be implemented with low loss using few optical components. We show that particular algorithms for simulating GBS are outperformed by high-dimensional GBS experiments at modest system sizes. This work thus opens the path to demonstrating QCA with programmable photonic processors.
ノイズと量子優位のフロンティア Noise and the Frontier of Quantum Supremacy
Adam Bouland; Bill Fefferman; Zeph Landau; Yunchao Liu
2021 IEEE 62nd Annual Symposium on Foundations of Computer Science Date Added to IEEE Xplore: 04 March 2022
DOI:https://doi.org/10.1109/FOCS52979.2021.00127
Abstract
Noise is the defining feature of the NISQ era, but it remains unclear if noisy quantum devices are capable of quantum speedups. Quantum supremacy experiments have been a major step forward, but gaps remain between the theory behind these experiments and their actual implementations. In this work we initiate the study of the complexity of quantum random circuit sampling experiments with realistic amounts of noise. Actual quantum supremacy experiments have high levels of uncorrected noise and exponentially decaying fidelities. It is natural to ask if there is any signal of exponential complexity in these highly noisy devices. Surprisingly, we show that it remains hard to compute the output probabilities of noisy random quantum circuits without error correction. More formally, so long as the noise rate of the device is below the error detection threshold, we show it is #P-hard to compute the output probabilities of random circuits with a constant rate of noise per gate. This hardness persists even though these probabilities are exponentially close to uniform. Therefore the small deviations away from uniformity are hard to compute, formalizing an important intuition behind Google’s supremacy claim. Interestingly these hardness results also have implications for the complexity of experiments in a low-noise setting. The issue here is that prior hardness results for computing output proba-bilities of random circuits are not robust enough to imprecision to connect with the Stockmeyer argument for hardness of sampling from circuits with constant fidelity. We exponentially improve the robustness of prior results to imprecision, both in the cases of Random Circuit Sampling and BosonSampling. In the latter case we bring the proven hardness within a constant factor in the exponent of the robustness required for hardness of sampling for the first time. We then show that our results are in tension with one another – the high-noise result implies the low-noise result is essentially optimal, even with generalizations of our techniques.
行列積演算子を用いた損失性ボソンサンプリングの古典的シミュレーション Classical simulation of lossy boson sampling using matrix product operators
Changhun Oh, Kyungjoo Noh, Bill Fefferman, and Liang Jiang
Physical Review A Published 5 August 2021
DOI:https://doi.org/10.1103/PhysRevA.104.022407
Abstract
Characterizing the computational advantage from noisy intermediate-scale quantum (NISQ) devices is an important task from theoretical and practical perspectives. Here, we numerically investigate the computational power of NISQ devices focusing on boson sampling, one of the well-known promising problems which can exhibit quantum supremacy. We study hardness of lossy boson sampling using matrix product operator (MPO) simulation to address the effect of photon loss on classical simulability using MPO entanglement entropy (EE), which characterizes a running time of an MPO algorithm. An advantage of MPO simulation over other classical algorithms proposed to date is that its simulation accuracy can be efficiently controlled by increasing an MPO’s bond dimension. Notably, we show by simulating lossy boson sampling using an MPO that as an input photon number grows, its computational cost, or MPO EE, behaves differently depending on a loss scaling, exhibiting a different feature from that of lossless boson sampling. Especially when an output photon number scales faster than the square root of an input photon number, our study shows an exponential scaling of time complexity for MPO simulation. On the contrary, when an output photon number scales slower than the square root of an input photon number, MPO EE may decrease, indicating that an exponential time complexity might not be necessary.