2024-07-23 京都大学
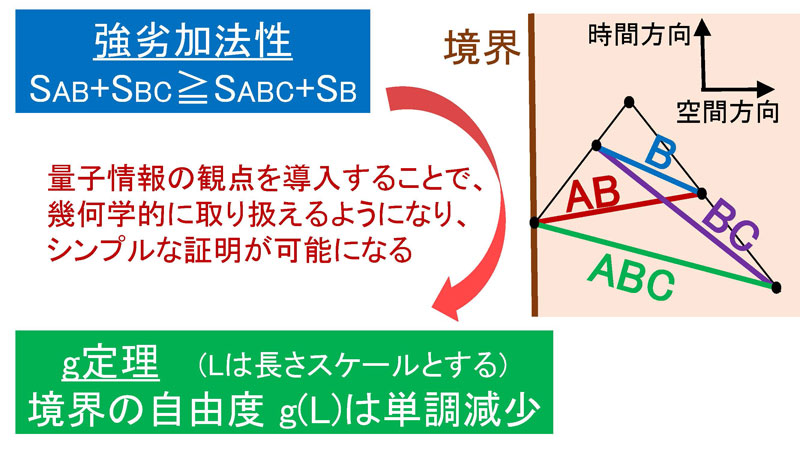
神田大樹 基礎物理学研究所博士課程学生、田耕健也 同修士課程院生、Jonathan Harper 同研究員、高柳匡 同教授の研究グループは、量子情報で基本的な不等式として知られる「強劣加法性」から、「1次元量子臨界点における境界の自由度はエネルギースケールを小さくするにつれて単調に減少する」というg定理と呼ばれる性質を幾何学的に導出することに成功しました。量子情報理論において、エンタングルメント・エントロピーは二体間の量子的な相関を測る重要な量ですが、強劣加法性と呼ばれる、三角不等式に類似した不等式を満たすことがよく知られています。本研究では、この強劣加法性を、1次元量子臨界点に対応する2次元共形場理論が境界を持つ場合に適用し、共形場理論におけるエンタングルメント・エントロピーの特徴的な振る舞いを巧妙に利用することで、境界を持つ共形場理論において最も基本的な性質と言えるg定理を明快に導出することができました。相互作用のある系において、量子論的な解析は一般に大変複雑です。しかし今回の研究では、量子情報理論の考察による幾何学的な視点からシンプルな証明を与えることができたことは画期的であり、こういった研究手法は今後、多方面への応用が期待されます。
本研究成果は、2024年7 月19 日に、国際学術誌「Physical Review Letters」にオンライン掲載されました。
研究者のコメント
「このg定理の強劣加法性からの証明は、問題自体は大変シンプルなのですが、トライするとすぐに行き詰る難問で、2007年から17年にわたってチャレンジしてきた問題です。しかし今回、ついにポスドク研究員や大学院生との刺激的な共同研究のおかげで、重要なトリックに気が付くことができました。そのおかげで、この問題をエレガントに解決することができ、大変うれしく思っています。今後はさらに、量子情報の不等式を物理学へ応用する例を増やしていきたいと思っております。」(高柳匡)
詳しい研究内容について
量子臨界点における境界自由度の単調性を量子情報から導出―量子エンタングルメントの三角不等式を用いた量子物質の幾何学的理解―
研究者情報
研究者名:田耕 健也
研究者名:Jonathan Harper
研究者名:髙柳 匡
書誌情報
【DOI】
https://doi.org/10.1103/PhysRevLett.133.031501
【書誌情報】
Jonathan Harper, Hiroki Kanda, Tadashi Takayanagi, Kenya Tasuki (2024). Theorem from Strong Subadditivity. PHYSICAL REVIEW LETTERS, 133, 3, 031501.