文字通りの「ひも理論」で自然ネットワークを解読（Scientists Use String Theory to Crack the Code of Natural Networks）

2026-01-07 レンセラー工科大学（RPI）

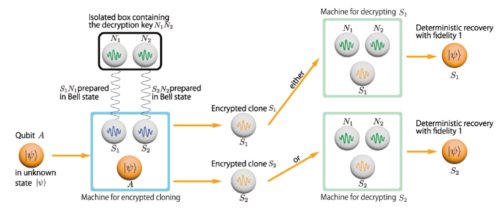
Natural physical networks are continuous, three-dimensional objects, like the small mathematical model displayed here. Researchers have found that physical networks in living systems follow rules borrowed from string theory, a theoretical physics framework. (Illustration by Xiangyi Meng/RPI)

＜関連情報＞

• https://news.rpi.edu/2026/01/07/scientists-use-string-theory-crack-code-natural-networks
• https://www.nature.com/articles/s41586-025-09784-4

表面最適化は物理ネットワークのローカル設計を左右する Surface optimization governs the local design of physical networks

Xiangyi Meng,Benjamin Piazza,Csaba Both,Baruch Barzel & Albert-László Barabási
Nature  Published:07 January 2026
DOI:https://doi.org/10.1038/s41586-025-09784-4

Abstract

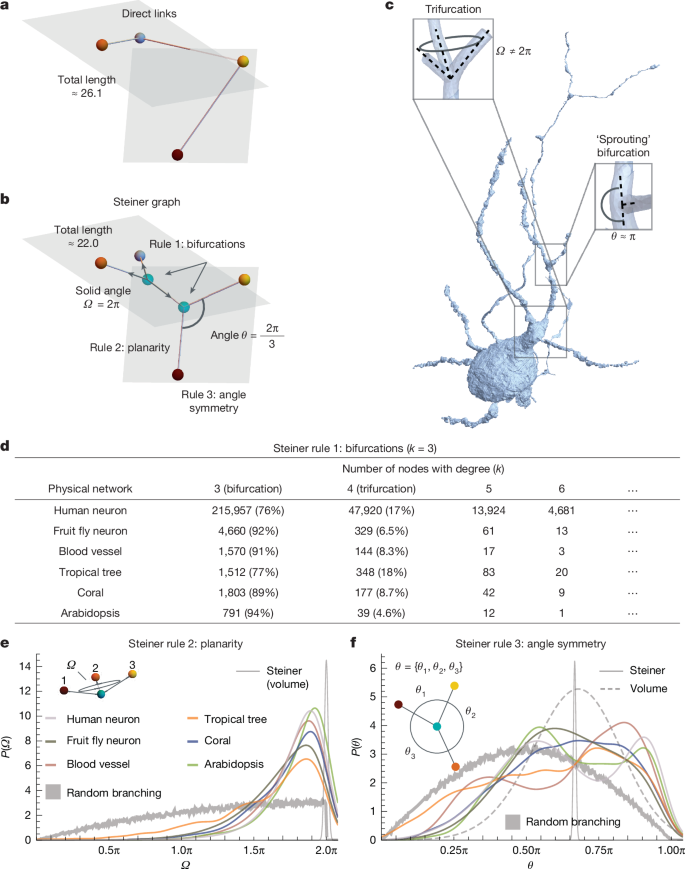
The brain’s connectome^1,2,3 and the vascular system⁴ are examples of physical networks whose tangible nature influences their structure, layout and, ultimately, their function. The material resources required to build and maintain these networks have inspired decades of research into wiring economy, offering testable predictions about their expected architecture and organization. Here we empirically explore the local branching geometry of a wide range of physical networks, uncovering systematic violations of the long-standing predictions of wiring minimization. This leads to the hypothesis that predicting the true material cost of physical networks requires us to account for their full three-dimensional geometry, resulting in a largely intractable optimization problem. We discover, however, an exact mapping of surface minimization onto high-dimensional Feynman diagrams in string theory^5,6,7, predicting that, with increasing link thickness, a locally tree-like network undergoes a transition into configurations that can no longer be explained by length minimization. Specifically, surface minimization predicts the emergence of trifurcations and branching angles in excellent agreement with the local tree organization of physical networks across a wide range of application domains. Finally, we predict the existence of stable orthogonal sprouts, which are not only prevalent in real networks but also play a key functional role, improving synapse formation in the brain and nutrient access in plants and fungi.