2025-07-23 東京科学大学
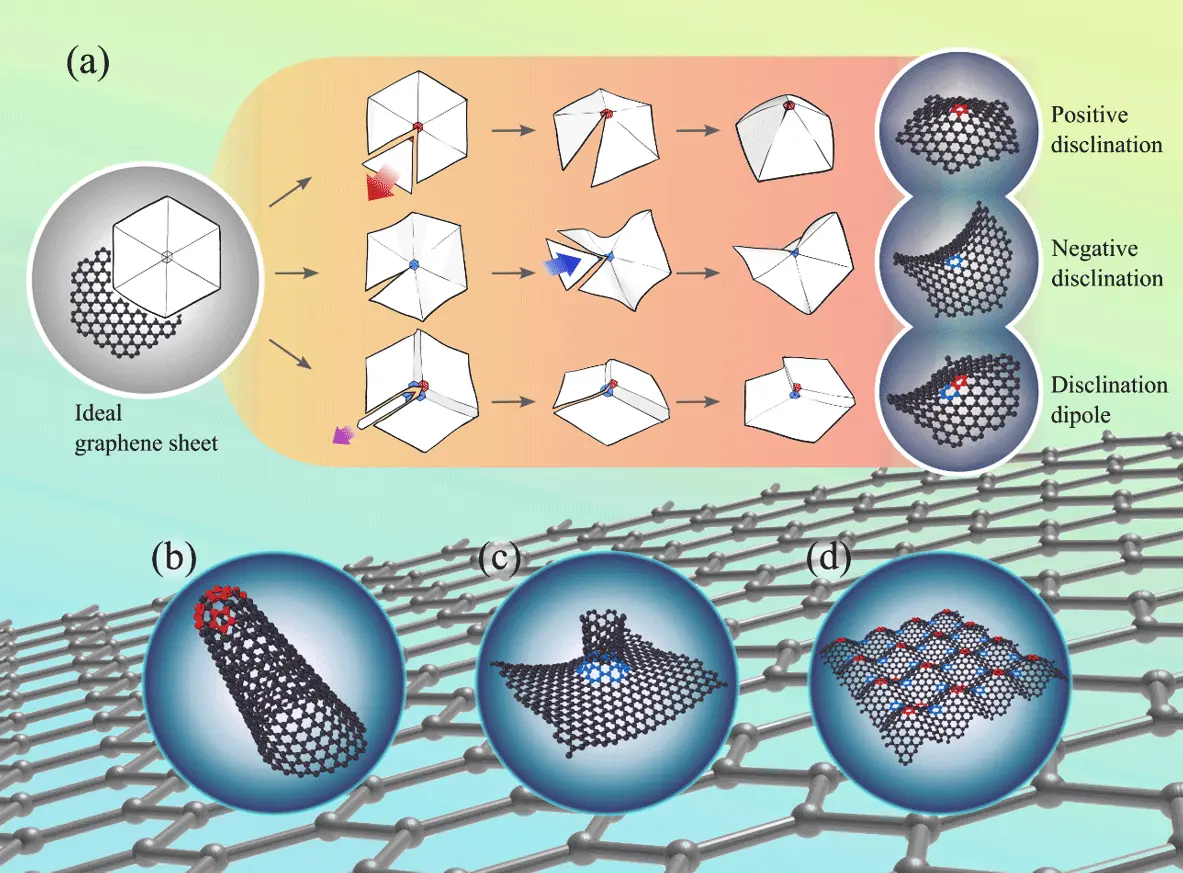
図1. （a）回位によるGSの切り紙モデルと分子動力学解析モデル。左端が理想的なGS（Ideal graphene sheet）。GSから60度の三角形領域を除去すると、正の回位（Positive disclination）が生じる。一方で、GSに60度の三角形領域を挿入すると、負の回位（Negative disclination）が生じる。GSの一部を局所的に押し込むことにより、GS内に回位双極子（Disclination dipole）が生じる。（b）カーボンナノホーン（CNH）、（c）GSとCNTのハイブリッド構造、（d）エッグトレイグラフェン。
＜関連情報＞
- https://www.isct.ac.jp/ja/news/ulpno86uc6um
- https://www.isct.ac.jp/plugins/cms/component_download_file.php?type=2&pageId=&contentsId=1&contentsDataId=1744&prevId=&key=8853d6afa73aecc805aa3f36b379605b.pdf
- https://pubs.rsc.org/en/content/articlelanding/2025/nr/d5nr01102g
グラフェンシートの曲げ剛性を評価するための、欠陥を組み込んだ新たな計算手法 A new computational approach for evaluating bending rigidity of graphene sheets incorporating disclinations
Yushi Kunihiro,Xiao-Wen Lei,Takashi Uneyama and Toshiyuki Fujii
Nanoscale Published:21 Jul 2025
DOI:https://doi.org/10.1039/D5NR01102G
Abstract
Two-dimensional (2D) materials exhibit remarkable flexibility and can be transformed into various shapes. Graphene sheets (GSs), in particular, can form conical or saddle-like shapes through the introduction of lattice defects known as disclinations, represented by 5- and 7-membered rings, respectively. These rotational-type lattice defects possess relatively large spontaneous curvature and significantly affect the bending rigidity of the GS. Despite increasing interests in exploiting such deformations for material design, evaluating the bending rigidity of GSs with lattice defects remains challenging owing to the complexity introduced by curvature and defect configurations. In this study, we propose a novel computational method that integrates the Helfrich theory of membranes with molecular-dynamics simulations to analyze the effect of curvature and defect patterns on the bending rigidity of GSs. This hybrid approach enables the direct evaluation of bending rigidity from atomic and geometric structures, eliminating the need for experimental bending tests. Using this method, we reveal, for the first time, contrasting trends in bending rigidity between GSs with monopole and dipole disclinations. In the presence of disclination monopoles, the bending rigidity remains independent of the specific structural pattern. Conversely, disclination dipoles, comprising both conical and saddle-shaped surfaces, induce local shape distortions that lead to localized variations in bending rigidity. These findings provide important guidelines for the design of 2D materials with specific bending rigidities, supporting the development of new materials.
