2025-06-27 京都大学
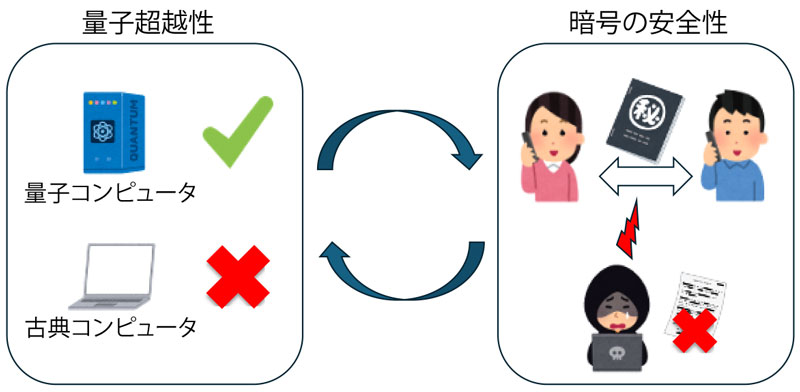
本研究では特定のタスクにおける量子超越性(左)の存在を証明するために暗号の安全性(右)を仮定することが必要十分であることを明らかにした。
<関連情報>
- https://www.kyoto-u.ac.jp/ja/research-news/2025-06-27
- https://www.kyoto-u.ac.jp/sites/default/files/2025-06/web_2506_Morimae-e37d3181d46ca75ce3c900689a8bd1da.pdf
- https://dl.acm.org/doi/10.1145/3717823.3718133
量子アドバンテージの暗号学的特性評価 Cryptographic Characterization of Quantum Advantage
Tomoyuki Morimae, Yuki Shirakawa, Takashi Yamakawa
STOC ’25: Proceedings of the 57th Annual ACM Symposium on Theory of Computing Published: 15 June 2025
DOI:https://doi.org/10.1145/3717823.3718133
Abstract
Quantum computational advantage refers to an existence of computational tasks that are easy for quantum computing but hard classically. Unconditionally showing quantum advantage is beyond our current understanding of complexity theory, and therefore some computational assumptions are needed. Which complexity assumption is necessary and sufficient for quantum advantage? In this paper, we show that inefficient-verifier proofs of quantumness (IV-PoQ) exist if and only if classically-secure one-way puzzles (OWPuzzs) exist. As far as we know, this is the first time that a complete cryptographic characterization of quantum advantage is obtained. IV-PoQ are a generalization of proofs of quantumness (PoQ) where the verifier is efficient during the interaction but may use unbounded time afterward. IV-PoQ capture various types of quantum advantage previously studied, such as sampling and search based quantum advantage. Previous work [Morimae and Yamakawa, Crypto 2024] showed that IV-PoQ can be constructed from OWFs, but a construction of IV-PoQ from weaker assumptions was left open. Our result solves the open problem, because OWPuzzs are believed to be weaker than OWFs. OWPuzzs are one of the most fundamental quantum cryptographic primitives implied by many quantum cryptographic primitives weaker than one-way functions (OWFs), such as pseudorandom unitaries (PRUs), pseudorandom state generators (PRSGs), and one-way state generators (OWSGs). The equivalence between IV-PoQ and classically-secure OWPuzzs therefore highlights that if there is no quantum advantage, then these fundamental cryptographic primitives do not exist. The equivalence also means that quantum advantage is an example of the applications of OWPuzzs. Except for commitments, no application of OWPuzzs was known before. Our result shows that quantum advantage is another application of OWPuzzs, which solves the open question of [Chung, Goldin, and Gray, Crypto 2024]. Moreover, it is the first quantum-computation-classical-communication (QCCC) application of OWPuzzs. To show the main result, we introduce several new concepts and show some results that will be of independent interest. In particular, we introduce an interactive (and average-case) version of sampling problems where the task is to sample the transcript obtained by a classical interaction between two quantum polynomial-time algorithms. We show that quantum advantage in interactive sampling problems is equivalent to the existence of IV-PoQ, which is considered as an interactive (and average-case) version of Aaronson’s result [Aaronson, TCS 2014], SampBQP≠SampBPP⇔ FBQP≠FBPP. Finally, we also introduce zero-knowledge IV-PoQ and study sufficient and necessary conditions for their existence.