量子観測に誘起されたスペクトル相転移の発見～平衡系と非平衡系との非自明な類似点～

2025-01-09 理化学研究所,東京大学

理化学研究所（理研）開拓研究本部濱崎非平衡量子統計力学理研白眉研究チームの濱崎立資理研白眉研究チームリーダー（理研数理創造プログラム上級研究員）、東京大学大学院工学系研究科物理工学専攻の望月健助教（理研開拓研究本部濱崎非平衡量子統計力学理研白眉研究チーム客員研究員）の共同研究チームは、観測下の量子系^[1]におけるスペクトル相転移^[2]を発見しました。

本研究成果は、近年急速に研究が進んでいる「非平衡な量子系における観測誘起相転移^[3]」と、古くから精力的に研究されている「平衡状態^[4]にある量子系における相転移」を、同一の枠組みで統一的に理解することにつながると期待されます。

共同研究チームは、Lyapunov解析^[5]という手法を用いることで、観測下の量子系においてもスペクトル相転移が存在することを示しました。また、その臨界点^[6]が量子もつれ^[7]転移の臨界点と一致することを見いだしました。

本研究は、科学雑誌『Physical Review Letters』オンライン版（1月8日付）に掲載されました。

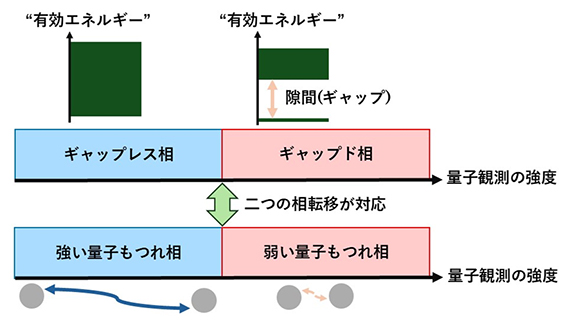
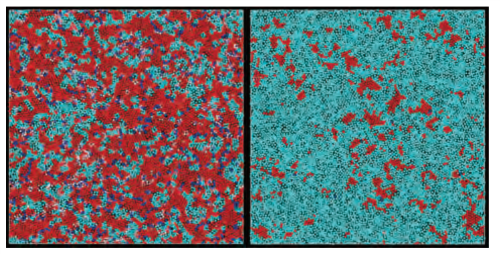
スペクトル相転移と量子もつれ転移の対応

背景

量子力学に従う系において、時間に依存しない平衡状態の振る舞いはハミルトニアン^[8]と呼ばれる行列（演算子）に完全に支配されます。そこで、ハミルトニアン行列のエネルギー固有値（スペクトル）やそれに対応した固有状態に基づく解析が古くから行われてきました。特に、ハミルトニアンのスペクトル相転移と量子もつれ転移が対応することが広く知られています。

スペクトル相転移とは、ハミルトニアンに含まれるパラメータを変化させた際、最も小さいエネルギー固有値（基底エネルギー）と、2番目に小さい固有値の差（ギャップ）に劇的な変化が起こることです。具体的には、系の体積を大きくしたときにギャップが減少し、最後にはゼロになるギャップレス相から、体積を大きくしてもギャップがゼロではない値にとどまるギャップド相へと変わります。

一方、量子もつれ転移とは、基底状態^[9]の量子もつれの度合いの体積依存性が変化することです。量子もつれの度合いはエンタングルメントエントロピーという量で定量化されます。例えば1次元系において、ギャップレス相では基底状態のエンタングルメントエントロピーが系の体積と共に増加しますが、ギャップド相では系の体積に依存しない値となることが知られています。平衡量子系の研究では、こうしたギャップと量子もつれの対応に基づき、磁性転移やトポロジカル相転移などのさまざまな興味深い現象が解析されてきました。

近年、観測下の非平衡な量子系において、新しいタイプの量子もつれ転移が存在することが明らかにされました。量子系の特徴として「観測するまで物理量の値が確定しない」という量子状態の重ね合わせがありますが、観測を行うと重ね合わせが急激に壊されてしまいます。この効果により、観測下の量子系における量子もつれ転移においては、平衡系における相転移では見られない興味深い性質が存在します。特に、（1）観測されていない量子系では粒子間の相互作用により量子もつれの度合いが時間発展と共に増大しますが、（2）観測すると量子状態の重ね合わせが壊れ、量子もつれの度合いを減少させます。この二つの効果の競合により、長時間後の量子もつれの度合いの体積依存性が変化します。1次元系の場合、観測が弱ければエンタングルメントエントロピーは系の体積に比例して増大し、遠く離れた粒子同士が強い量子もつれを発現する相が実現します。一方、観測が強ければエンタングルメントエントロピーは系の体積を増やしても増加せず、量子もつれの弱い相が実現します。量子もつれや相転移現象、観測が量子系に与える影響はいずれも古くから調べられてきた重要な研究対象です。そのため、近年発見された観測誘起量子もつれ転移はさまざまな観点から精力的に研究されており、量子コンピュータによる実験も行われています。

従来研究されてきた平衡系における量子相転移と、まだ謎の多い観測誘起量子もつれ転移に共通の性質は何なのか、また両者の質的な差異は何であるか、という問いはさまざまな相転移現象を統一的に理解する上で重要です。従来の平衡系における量子相転移はハミルトニアンのスペクトル相転移として理解できます。従って、観測誘起相転移をスペクトルの観点から解析できれば、両者の比較が容易になり、非平衡系での量子相転移現象に対する理解が進むと考えられます。

しかし、観測下の量子系においてスペクトル解析の手法は発展していませんでした。これは、量子観測では量子揺らぎにより観測結果がランダムになり、平衡系におけるハミルトニアンのような系の挙動を完全に記述する行列が存在しないためです。そのため、観測下の量子系においてスペクトル相転移が起こるのか、またその臨界点が平衡系と同様に量子もつれ転移と対応するのかは分かっていませんでした。

研究手法と成果

本研究ではまず、量子観測に誘起される観測結果のランダムなダイナミクスにLyapunov解析を適用し、有効ハミルトニアンを定義しました。これにより、（1）観測下の量子ダイナミクスにおいて、長時間後の量子状態が有効ハミルトニアンの基底状態へ緩和すること、（2）その緩和時間が有効ハミルトニアンのスペクトルギャップにより決定されること、を見いだしました。ここで、平衡系の挙動を記述する通常のハミルトニアンと同様に、スペクトルギャップは、有効ハミルトニアンの最小”有効エネルギー”と2番目に低い”有効エネルギー”の差（ギャップ）として、基底状態は最小の”有効エネルギー”に対応する固有状態として定義します。有効ハミルトニアンの導入により、平衡量子系における相転移と観測下の量子系のような非平衡量子系における相転移の詳細な比較が可能となりました（図1）。もともとLyapunov解析は、古典非線形力学系におけるカオス的な時間発展を解析するために発展した手法です。古典系の解析手法がランダムな時間発展をする量子系に自然に適用できるという観点からも、本研究の成果は興味深い結果であると考えられます。

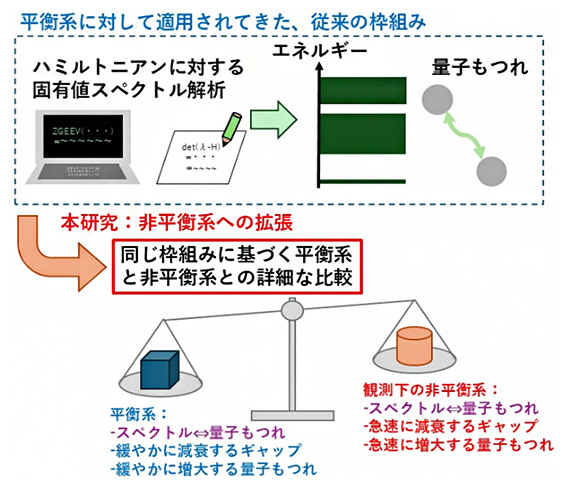
図1 平衡系で古くから用いられてきた手法の非平衡系への拡張
平衡系では、紙と鉛筆を使った手計算やコンピュータによる数値計算でハミルトニアンのスペクトル解析を行い、エネルギーや量子もつれを求めるという手法が古くから用いられてきた。観測下の量子系のような非平衡系に対してはエネルギースペクトルに基づく解析が困難だと考えられてきたが、本研究により平衡系と同様の解析が可能となった。この共通の枠組みを通じて平衡系の知見からヒントを得ることで、非平衡状態にある量子系の理解が進むと期待される。

次に、Lyapunov解析で得られたスペクトルを詳細に解析することで、（1）観測を強めた際にギャップレス相からギャップド相へのスペクトル相転移が起こること、（2）基底状態の量子もつれ転移が起こり、その臨界点がスペクトル相転移の臨界点に一致することを示しました。1次元系のギャップレス相ではエンタングルメントエントロピーは系の体積と共に増加しますが、ギャップド相では体積に依存せず一定の値となります。この結果は、量子もつれのような粒子間の相関とスペクトルギャップとの間の対応が、平衡状態にある量子系だけでなく、観測下の量子系などの広範な非平衡系でも成り立つことを示唆しています。なおスペクトル相転移は、量子もつれ転移との一致だけではなく、「完全混合状態が純粋状態へと緩和する時間スケールが劇的に変化する」転移として注目されていた純粋化転移とも対応することが示されます。

さて、スペクトル相転移と量子もつれ転移との一致が平衡系と観測下の量子系の非自明な類似点であることを述べてきましたが、同時に本研究ではこれらの系の違いについても調べました。特にギャップレス相において、スペクトルギャップとエンタングルメントエントロピーが系の体積にどのように依存するかが著しく異なることを見いだしました。すなわち、系の体積を増やしたとき、観測下の量子系におけるスペクトルギャップは典型的な平衡系の場合に比べて非常に速く（指数関数的に）小さくなります。また、観測下の量子系においてエンタングルメントエントロピーは典型的な平衡系での値よりも速く（線形に）増大します（図1）。これらの結果は、平衡系と非平衡系の本質的な違いを理解するのに役立つことが期待されます。

今後の期待

本研究から、ハミルトニアンの固有値と固有状態に基づいて現象を理解するという平衡系で確立したパラダイム（枠組み）が、Lyapunov解析を通じて、非平衡量子系でも有効であることが分かりました。そのため、本研究の成果はさまざまな量子系を同一の枠組みに基づいて統一的に理解することにつながると予想されます。これにより、平衡系の研究から蓄積された膨大な知見に基づく新奇な非平衡現象の予言や、平衡系では起こり得ない非平衡系特有な現象の発見が期待されます（図1）。

補足説明

1.観測下の量子系
外界から孤立した量子系で見られるような粒子間の相互作用による時間発展の最中に、粒子の観測が行われる量子系。量子観測すると粒子の状態の量子的重ね合わせが壊れる。この効果により、孤立量子系では自然に起こる粒子同士の量子相関の発達や平衡状態への緩和が妨げられる。

2.相転移
系のパラメータを変化させた際、ある値を境に系の性質が劇的に変化する現象。温度を変化させた際に物質が磁石状態からそうではない状態へと変わる磁性転移などが代表例である。絶対零度において温度以外のパラメータを変化させると、基底状態の相転移である量子相転移が起こり得る。系の体積が大きくなるにつれて相転移の特徴がより顕在化する場合が多いため、相転移現象を解析する際は物理量の体積依存性がよく調べられる。

3.観測誘起相転移
量子観測の強さを変化させた際に起こる相転移現象。観測すると重ね合わせなどの量子的性質が壊れるため、観測が強い場合は量子もつれが弱い相が実現し、観測が弱い場合は量子もつれが顕著に現れる強い量子もつれ相が実現される。

4.平衡状態
時間的に変動せず、温度やエネルギーなどの少数の物理量のみにより特徴付けられる状態。平衡状態にある量子系に関する解析手法は高度に発達しており、それを基に多くの重要な現象が明らかにされてきた。一方、平衡状態から外れた非平衡状態にある量子系の解析手法は発展途上である。

5.Lyapunov解析
古典力学系における非線形な時間発展を研究するために発達したスペクトル解析の手法。Lyapunov解析に基づき、古典非線形力学系におけるカオス転移などの重要な現象が明らかにされてきた。本研究では、古典非線形系に対して用いる場合とは少し異なる形式で、Lyapunov解析を量子系に適用した。

6.臨界点
相転移現象において、系の性質が劇的に変化する境目のパラメータ値。相転移の臨界点付近では、系のミクロな詳細によらずに共通の性質（相関関数の減衰の挙動など）が現れることが知られている。そのような事実は「普遍性」と呼ばれ、相転移を研究する上で重要な研究対象の一つである。

7.量子もつれ
複数の粒子の間に存在する、特殊な相関（量子相関）。このような相関は量子力学によって説明され、ニュートン力学で記述される古典力学に従う系には存在しない。低温で強い量子もつれのある量子系は、古典系とは大きく乖離（かいり）した振る舞いを示す場合が多い。

8.ハミルトニアン
量子系の振る舞いに対し重要な役割を果たす行列（演算子）。ハミルトニアンの固有値スペクトルから系のエネルギーを求めることができる。また、平衡状態にある量子系の挙動はハミルトニアンの固有値スペクトルから理解できる。

9.基底状態
エネルギー固有値が最も低いハミルトニアンの固有状態。絶対零度における平衡状態ということもできる。基底状態は量子効果を顕著に示すため、平衡状態にある量子系において特に重要な状態である。平衡量子系では、低温になるほど基底状態の性質が強く反映される。

研究支援

本研究は、日本学術振興会（JSPS）科学研究費助成事業若手研究「複雑性指標に基づく開放量子系のダイナミクス及び相転移に関する研究（研究代表者：望月健）」「量子多体系における速度限界の解明およびその制御への応用（研究代表者：濱崎立資）」、科学技術振興機構（JST）戦略的創造研究推進事業ERATO「沙川情報エネルギー変換プロジェクト（研究代表者：沙川貴広、JPMJER2302）」による助成を受けて行われました。