2023-07-18 東京大学,京都大学
発表のポイント
- 正逆いずれの方向へも進行しうる可逆な化学反応のみから構成される反応ネットワークにおいて、無数の候補の中から、いかにして目的の生成物に向かう反応経路が選択されるのかという、経路選択の原理を解明しました。
- タンパク質の折り畳みや分子自己集合など、多数の化学反応が複雑に連結したネットワーク構造は自然界に遍く存在し、適応性や頑健性などの機能は、こうしたネットワークにおける複数の反応間の協働に由来すると考えられています。今回、ネットワーク構造の役割の一つとして、ある反応段階が不可逆に振る舞うことが明らかになりました。
- 個々の反応ではなく、それらが連結したネットワークを包括的に理解することで、単純な足し合わせでは表せない非線形現象の解明への貢献が期待されます。
可逆反応ネットワークにおける経路を選択する原理
発表内容
東京大学大学院総合文化研究科の平岡秀一教授と、京都大学大学院工学研究科の佐藤啓文教授らによる研究グループは、可逆な化学反応ネットワークの中のある反応過程が準不可逆になることで、ネットワーク中の反応経路が選択され、準安定な速度論状態(注1)を作り出すこともできることを明らかにしました。
〈研究の背景〉
反応ネットワークは、幾つもの素反応(注2)が互いに繋がりネットワーク構造を形成し、代謝ネットワークや神経ネットワークなど、生命活動に欠かせない重要な機能を担っています。これらの反応ネットワークの特徴は、ネットワークを構成する素反応が比較的単純であるにもかかわらず、これらを複雑に繋ぐことで、それぞれの素反応の特徴の足し合わせからは予想できない現象が発現することです。素反応には可逆反応と不可逆反応(注3)があり、可逆反応は双方向に進行可能ですが、不可逆反応は片側のみ進行します。これまで研究対象とされてきた反応ネットワークの多くは不可逆な素反応からなるもので、可逆な素反応のみから構成される「可逆な反応ネットワーク」における振る舞いに関する研究はありませんでした。その主な理由は、可逆な素反応は、途中経過がどうあれ最終的に化学平衡状態(注4)に至るため、可逆な反応ネットワークにおける振る舞いも本質的に化学平衡へ至り、それぞれの素反応がどちら向きに進行し、ネットワーク内のどの経路が選ばれるのかということに対する関心が低いためです。一方で、可逆な反応ネットワークで化学平衡状態に至らない系も知られています。速度論トラップ(注5)と呼ばれる予期しない準安定種を与える場合で、タンパク質の折り畳みや集合化にみられることがあります。これまで、速度論トラップの生成は、その高い速度論安定性(注6)に由来すると説明されてきました(図1)。しかし、たとえ速度論トラップの安定性が高くても、そもそもそこへ至る経路が選択されなければ、生成されることもありません。つまり、速度論トラップの生成に対する真の理解には、経路選択の解明が不可欠ですが、これまで可逆な反応ネットワークにおける経路選択の原理は明らかにされていませんでした。
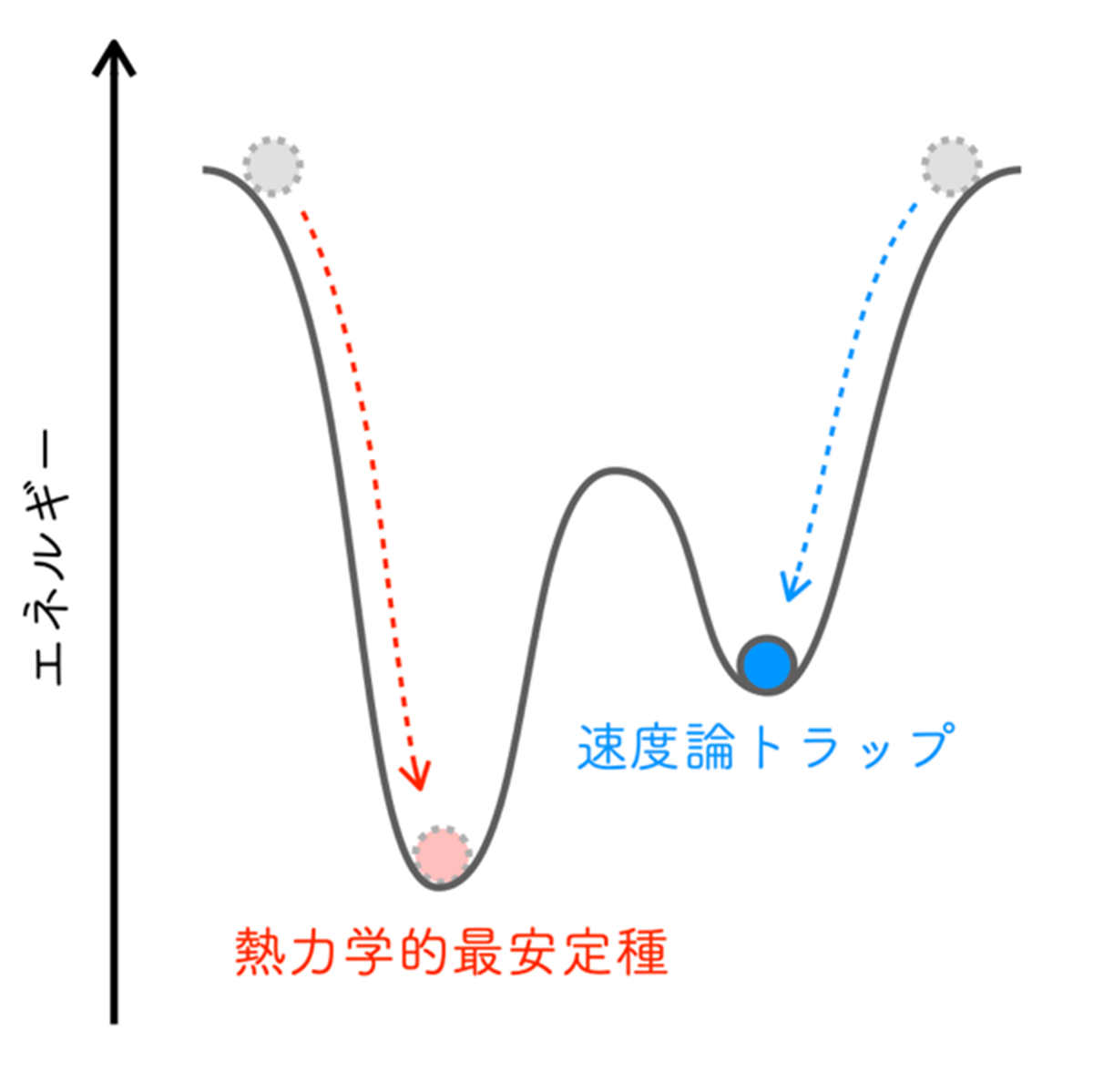
図1:速度論トラップのイメージ図速度論トラップは熱力学安定種への変換のエネルギー障壁が高いためにトラップされた準安定種である。反応が赤の破線矢印を経て進行すると速度論トラップに至らない。速度論トラップの形成はそれに至る経路(青の破線矢印)の選択も重要な要素である。
〈研究の内容〉
本研究では、可逆な反応ネットワークで起こる現象を解明する手立てとして、数理モデルによる反応解析を行いました。数理モデル解析により、さまざまな自然現象に対する一般原理や普遍原理を明らかにすることができます。まず初めに、Curtin-Hammett原理(注7)と呼ばれるたった3つの素反応からなる単純な系に適用される原理を出発点として、順に複雑な反応ネットワークへ発展させました。Curtin-Hammett原理は、速い可逆な素反応(A ⇄ B)の両端に遅い不可逆反応(A → C、B → D)が接続された場合、反応の帰結は2つの不可逆反応の活性化エネルギーで決まり、速い可逆反応(A ⇄ B)は関与しないというものです(図2a)。まず初めに、2つの不可逆反応の活性化エネルギーを下げ、A → Cの速度定数をA → Bの速度定数と同じにしたところ、Curtin-Hammett原理に近い振る舞いをすることがわかりました(図2b)。続いて、A-C間とB-D間の反応を可逆反応に変更しました(図2c)。この状態では3つの可逆反応(A ⇄ B、A ⇄ C、B ⇄ D)が繋がっているため、最終的に系は化学平衡状態に到達し、エネルギーダイアグラムで最安定なDが主生成物になるはずです。数値シミュレーションを行うと、確かに反応の収束状態(図2cの1,000分)で、DがCよりも多く生成し、その比は3つの素反応の平衡定数から計算された値と等しくなりました。しかし、収束状態へ至る途中で、一過的にCurtin-Hammett原理が発現しCがDよりも多く生成する状態(一過的な速度論状態)を形成することが明らかになりました。続いて、A ⇄ Cと全く同じ反応をCとDに接続した5つの可逆反応からなるネットワークを構築しシミュレーションを行うと(図2d)、一過的な速度論状態が40分から1.4日へ劇的に長寿命化することが明らかになりました。これらの結果から、可逆な反応ネットワークにおいても速度論の支配により一過的な速度論状態を作り出すことが可能で、可逆反応を増やすことでその寿命を延ばすことができることもわかりました。
続いて、準不可逆性の発現が反応経路の選択を導くことを見るために、多数の可逆な素反応が網目状に繋がり、枝分かれし、化学結合の組み換えに対応する分子間反応も含む、分子自己集合系(注8)をモデル化した複雑な反応ネットワークでの数値シミュレーションと解析を行いました。本研究で取り上げた分子自己集合は、Pd2+錯体と有機三座配位子LからなるPd6L4切頂四面体錯体で、この構造内には3つのLが三角形を作る部分と4つのLから四角形を作る部分構造が存在します(図3a)。Pd6L4を形成するためには、分子内でL同士をPd2+を介して連結する分子内反応が3回起こる必要があり、経路1:四角形→三角形→三角形と経路2:三角形→三角形→三角形の二通りが考えられます。そのため、上記の素反応を直列につないだ場合のように(図2)、最終生成物が異なるわけではありませんが、経路1と2のどちらを選択するかを調べることで、経路選択に関する議論が可能です。本分子自己集合を実験的に追跡し、自己集合過程を実験および数理モデルによって解析する手法(QASAP: Quantitative Analysis of Self-Assembly Process(注9)、NASAP: Numerical Analysis of Self-Assembly Process(注10))による反応ネットワーク内の素反応の最適な速度定数を決定しました。
得られた速度定数をもとに自己集合をシミュレーションした結果、経路1が主要反応経路であることが分かりました。次に、なぜ経路1が選択されたのかを調べるために、経路1と経路2に関わる主要経路を比較したところ、反応開始60分から80分頃までは経路2が優勢で、その後経路1に反転することが明らかになりました(図3b)。また、この反応の進行方向の反転現象は、経路1の中にある2つの素反応が準不可逆となっていることが原因であることが分かりました。興味深いことに、これらの素反応の速度定数(k3: k3f, k3b)は同程度の大きさのため、速度定数から片側のみへ進行するような振る舞いを予測できません。また、経路2の中にも同じ速度定数(k3f, k3b)をもつ素反応が存在しますが、その素反応では準不可逆性は発現しませんでした。これらの結果から、自己集合のような複雑な可逆反応ネットワークでは、ある素反応がその速度定数とは無関係に準不可逆性を発現することがあり、この準不可逆性の発現が経路選択の鍵であることが明らかになりました。この準不可逆性は、素反応をネットワークから取り出しても見られず、ネットワーク内で他の素反応と複雑に相互作用することではじめて現れる非線形現象であり、さらに素反応の進行方向までも変化することが明らかになりました。
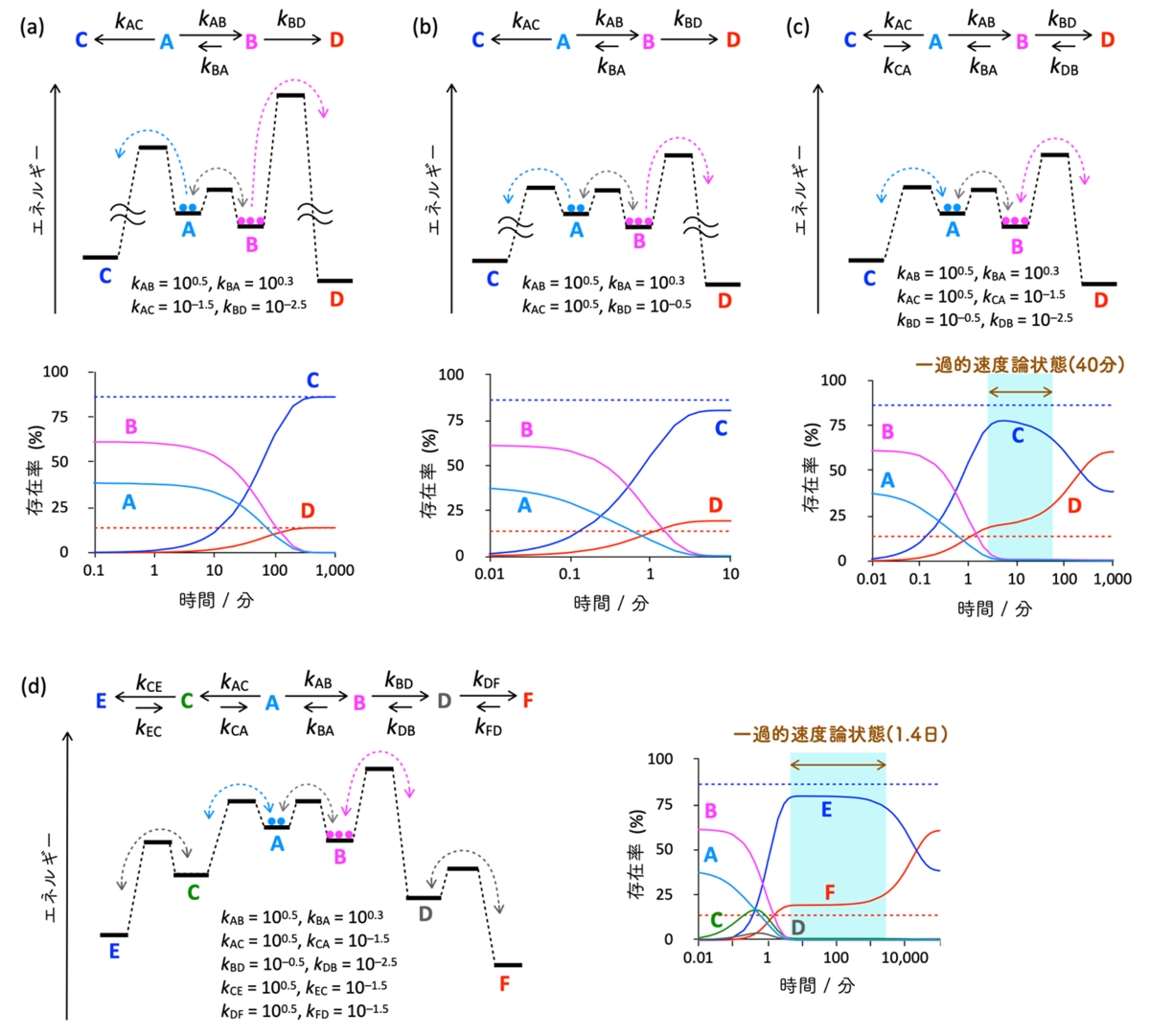
図2:Curtin-Hammett原理の拡張における数理モデルシミュレーション(a) 厳密なCurtin-Hammett条件における数値シミュレーション。可逆反応(A ⇄ B)は不可逆反応(A → C、B → D)に比べ十分に速い。生成物C、Dの生成比は不可逆反応により決まる。青と赤の破線はCurtin-Hammett原理によるCとDの生成率の計算値を示す。
(b) 厳密なCurtin-Hammett条件に対して、不可逆反応(A → C、B → D)のエネルギー障壁を下げた場合の数値シミュレーション。生成物C、Dの生成比は厳密なCurtin-Hammett条件に近い。
(c) (b)の条件における不可逆反応を可逆反応(A ⇄ C、B ⇄ D)とした場合の数値シミュレーション。全ての素反応が可逆なため、最終的に化学平衡に到達し、その時熱力学的に安定なDがCよりも多く生成するが、Curtin-Hammett原理に従って一過的速度論状態が作り出されることがわかった。
(d) (c)の反応ネットワークのCおよびDにA ⇄ Cと同じ素反応を接続した5つの可逆な素反応からなるネットワークにおける数値シミュレーション。化学平衡状態における生成物EとFの比率は(c)と変わらないが、可逆反応を増やしたことで、一過的速度論状態の寿命が40分から1.4日に延びた。可逆な素反応のみからなる反応ネットワークでも、速度論の支配を受けCurtin-Hammett的振る舞いをすることが明らかになった。
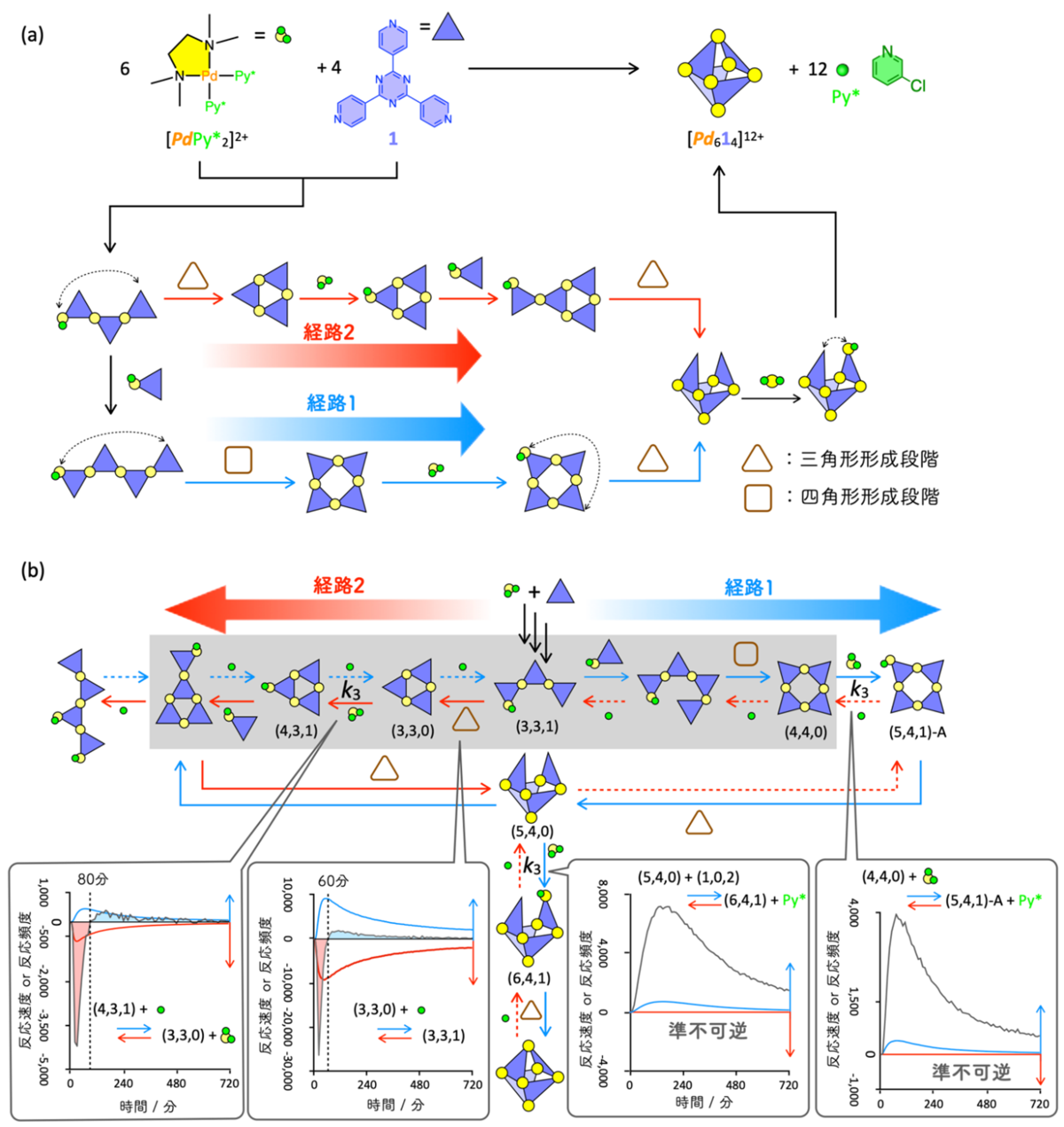
図3:多数の素反応からなる複雑な反応ネットワークの一例として扱った自己集合体の形成における準不可逆性の発現による経路選択(a) Pd(II)錯体([PdPy*2]2+)および三座配位子(L)からなる[Pd6L4]12+切頂四面体の自己集合と3回の分子内反応に着目した2種類の自己集合経路。実験データに対する数理モデル解析によって経路1が主要経路であることが明らかになった。
(b) 経路1および2における反応の進行方向および準不可逆性に関する解析結果。経路2上にある反応((3,3,1)→(3,3,0)と(3,3,0)→(4,3,1))では、60分、80分まで赤矢印の方向へ反応が進行するが、その後進行方向が逆転する(左側の吹き出しの中の赤と青で塗った部分は反応頻度を表す)。一方、経路1上にある反応((4,4,0)→(5,4,1)-Aと(5,4,0)→(6,4,1))では、赤の破線矢印方向の反応速度が0となり準不可逆として振る舞う(反応速度が0であることを示す赤線)。これらの反応速度定数はk3 (k3f, k3b) で、同じ速度定数が経路2の(3,3,0)→(4,3,1)にも割り当てられているにもかかわらずその振る舞いは大きく異なる。このことから、準不可逆性の発現は素反応の速度定数で決まるものではなく、他の素反応との相互作用による非線形現象として現れたことを示している。
〈今後の展望〉
可逆反応は熱力学支配に従うため経路に無関係である、というこれまでの考え方に対して、本研究により、複数の可逆反応がつながった反応ネットワークでは、ある反応段階に準不可逆性が発現することで、一過的な速度論状態が形成され、これがネットワーク内の各素反応の相互作用に起因することが明らかになりました。可逆な反応ネットワークは、素反応の進行方向までも変化しうるため、環境変化に対するシステムの適応現象や頑健性の発現など、生命システムをはじめとするネットワーク構造の役割のさらなる理解に役立つと期待されます。また、本モデル系は各素反応が速度定数というパラメータのみで特徴づけられているにも関わらず、準不可逆性という非線形現象が現れたことから、非線形現象の本質の解明にも役立つと期待されます。
発表者
東京大学 大学院総合文化研究科 広域科学専攻 相関基礎科学系
平岡 秀一(教授)
高橋 聡(助教)
阿部 司(助教)
京都大学 大学院工学研究科 分子工学専攻
佐藤 啓文(教授)
論文情報
雑誌:Chem(オンライン版:7月18日付)
題名:Pathway bias and emergence of quasi-irreversibility in reversible reaction networks: extension of Curtin-Hammett principle
著者:Satoshi Takahashi, Tsukasa Abe, Hirofumi Sato, and Shuichi Hiraoka*
DOI:10.1016/j.chempr.2023.06.015
研究助成
本研究は、科研費「自己集合過程の解明に基づく準安定な自己集合体の開発(課題番号:19H02731)」、「キラルセルフソーティングの機構解明(課題番号:19K22196)」、「反応ネットワークに基づく分子自己集合過程の解明(課題番号:20K05417)」、「速度論支配下で働く配位自己集合の原理の解明(課題番号:21K18974)」、「速度論支配による多成分自己集合性錯体の創成(課題番号:23H01970)」、旭硝子財団の支援により実施されました。
用語説明
(注1)速度論状態
化学反応の進み具合の時間的変化に関する法則を論じる学問分野を速度論という。反応が進行するために乗り越えなければならないエネルギー障壁の高さに関係付けられる反応速度定数を基にして化学反応を議論する。系全体がエネルギー的に最も安定な、最低エネルギーの状態(熱力学支配の状態といい、どれだけ時間が経過してもその状態が保たれる)に到達しておらず、エネルギーの高い状態にも分子が分布することを、速度論状態とよぶ。
(注2)素反応
ひとつ以上の化学種が、遷移状態を通過して(エネルギー障壁を越えて)一段階で生成物を導く反応のこと。
(注3)可逆反応と不可逆反応
反応物から生成物が生成する反応と、反対向きに戻る反応がともに起こり得る反応のこと。前者と後者をそれぞれ正反応と逆反応とよび、前者しか起こらない反応を不可逆反応とよぶ。
(注4)化学平衡状態
可逆反応において、正反応と逆反応が同じ速度で進行している状態のこと。反応系全体では、見かけ上何の変化も起こっていないように見える。
(注5)速度論トラップ
大域的な反応の途上にエネルギー障壁が高い素反応が存在すると、反応ネットワークが可逆であっても化学平衡に至らない場合があり、そのときに得られる化学種を速度論トラップとよぶ。
(注6)速度論安定性
系全体がエネルギー的に最も安定ではない状態にある場合の安定性のこと。速度論安定性の高い状態は準安定とよばれ、時間の経過、或いは外部条件の微小な変化に応じて別のより安定な状態へと変化する。一方で、系全体がエネルギー的に最も安定、つまり最低エネルギーの状態にあるときの安定性のことを、熱力学的安定性という。熱力学的安定性が高ければ、どれだけ時間が経過してもその状態が保たれる。化学平衡状態においては、熱力学的に最も安定な状態にある分子の数が最も多く、エネルギーの高い状態にある分子ほど分布する個数が少なくなる。
(注7)Curtin-Hammett原理
化学反応速度論における基本原理のひとつであり、基礎概念は1950年にLouis Plack Hammettによって提案され、1954年にその重要性がDavid Yarrow Curtinによって適切に認識されたことによる。図2(a)に示されるスキームの化学反応において、A-B間の可逆反応が速くA→CとB→Dの不可逆反応が遅い場合、生成物CとDの比は基質AとBの相対的な割合、つまりkAB/kBAのみによって決定されるのではなく、2つの不可逆反応のエネルギー障壁における差(kACとkBDの大小関係)によって制御される。古くはAとBが配座異性体である有機分子の安定性解析において広く適用された。図2(a)の例では[C]/[D] = (kAC × kBA)/(kAB × kBD) = (10-1.5 min-1 × 100.3 min-1)/(100.5 min-1 × 10-2.5 min-1) = 100.8 = 6.3となり、Bの存在率が高いにもかかわらずCが主生成物になる。A-C間とB-D間の反応も可逆である場合には、[C]/[D]はCとDの熱力学的安定性によって決定され、kCA > kDBならばDが主生成物となり、図2(c)の化学反応の場合、[C]/[D] = (kAC × kBA × kDB)/(kBD × kAB × kCA) = 10(0.5+0.3-2.5) -(-0.5+0.5-1.5) = 0.63となる。
(注8)分子自己集合
特定の反応条件の下で、構成要素分子が自発的に特定の構造をもつ物質へと集合する現象。しばしば、生体関連物質や人工物質が機能を発現する源となる。
(注9)QASAP (Quantitative Analysis of Self-Assembly Process)
分子自己集合過程を実験によって解析する手法。全ての基質と生成物の時間発展を核磁気共鳴分光法によって直接的に追跡・定量し、全ての中間体の平均組成の時間発展から自己集合過程に関する情報を得ることができる。一般的に分子自己集合の過程で生成する全ての中間体を観測することは不可能だが、本手法では、追跡が可能な基質と生成物の情報から全中間体の情報が間接的に得られるため、自己集合機構の議論に有効である。
(注10)NASAP (Numerical Analysis of Self-Assembly Process)
自己集合過程を数理モデルと数値計算によって解析する手法。反応途上で生成が予想される化学種とそれらの間の素反応を全て考慮した大域的な反応ネットワークを構築し、ネットワーク内の各素反応に速度定数を割り当て、QASAPで得られたデータへのフィッティングを通して決定した反応速度定数値から詳細な反応過程を解析し、反応経路を決定する。実験のみでは追跡できない反応領域の振舞いを詳細に解析できる。