2023-02-14 東京大学

発表者
嶋本 大祐(東京大学 大学院総合文化研究科 広域科学専攻 修士課程)
柳澤 実穂(東京大学 大学院総合文化研究科 広域科学専攻/大学院理学系研究科 物理学専攻 准教授)
発表のポイント
- 極端に大きさがばらついた粒子をランダムに詰め込んだ際の、ばらつきによらない共通した構造と、より密に詰め込むためのばらつきの条件を発見しました。
- 大きさが極端にばらついた粒子集団では、個々の粒子の大きさの影響が弱まることで、粒子全体のばらつきにはよらない共通した構造が現れることを見出しました。
- 岩石や土砂の粒、生物細胞に含まれる分子など、ばらつきが極めて大きな粒子が密に詰め込まれた系の理解や構造の制御に貢献すると考えられます。
発表概要
極端に大きさがばらついた粒子がランダムに詰め込まれた構造は、目にみえる岩石や土砂の粒から目にはみえない細胞に含まれる分子まで、自然界に広く見られます。こうした構造の特性を明らかにすべく研究が進められてきましたが、自然界にみられる系のような、極めて大きなばらつきが密な構造へ及ぼす影響は理解が進んでいませんでした。
東京大学大学院総合文化研究科の嶋本大祐大学院生と柳澤実穂准教授は、粒子の大きさのばらつきが極端に大きい例として、大きさが「べき分布」にしたがう円形粒子をランダムに詰め込んだ際の構造を実験の数値計算から調べ、ばらつきがもたらす特有の性質を明らかにしました。各粒子が他の粒子と接している点の個数の分布が、粒子の大きさの分布(ばらつき)によらないことや、より密な構造をつくるばらつきの条件を見出しました。
今回の発見は、自然界にみられる土砂や細胞内分子などを、極端に大きさがばらついた粒子集団とみなすことで、ばらつきの背後に潜む系に共通した構造や性質の発見につながることが期待されます。
本研究成果は、2023年2月10日(米国東部時間)に「Physical Review Research」のオンライン版で公開されました。
発表内容
研究の背景・先行研究における問題点
岩石や河原の砂利、瓦礫、石鹸の泡、細胞内の分子にいたるまで、大きさにばらつきをもつ粒がランダムに詰め込まれた構造は、いろいろな場面で目にします。こうした粒子集団のふるまいを理解するために研究が進展してきましたが、すべての粒子が同じ大きさの場合や、2種類の大きさの粒子を混合した場合のように、ばらつきが小さな系を考えることが多く、自然界で見られるようなばらつきの度合が非常に大きな系のふるまいは未解明でした。
研究内容
本研究では、先行研究とは逆に大きさが極端にばらついた系に注目し、大きさがべき分布にしたがう粒子集団(注1)を扱うことにしました(図1a)。この粒子集団では、大きさが半分の粒子は2倍の個数存在する、というような設定で、小さい粒子ほど多くなります。また、大きさがべき分布となる粒子集団は、衝撃による破壊などの現象の結果としても生じることから、岩石や土砂の粒などに見られることが知られています。
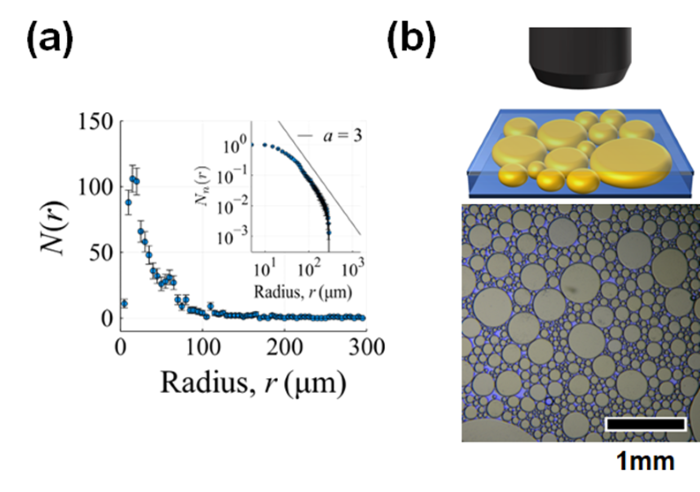
図1:(a)べき分布の例。円形粒子の半径 がr-3にしたがう分布。(b)大きさがバラバラな円形粒子を平面内で密に詰め込んだ際の模式図(上)と、実際に上から撮影した顕微鏡画像(下)。
本研究では、実験とコンピュータシミュレーションの両方を用いて、大きさがべき分布にしたがう円形粒子をランダムに詰め込んだ際の構造を調べました。実験では、水の中にいれた油の粒を繰り返し壊し小さくすることで、大きさがべき分布に従う粒子集団を準備しました。それを、狭い板の間にランダムに配置し、外側にある水の蒸発により、ゆるやかに圧縮された際の密な構造を解析しました(図1b)。シミュレーションでは、互いに反発する円形粒子を平面上でランダムに配置し、実験と同じく緩やかに圧縮することで粒子を詰め込みました。大きさのばらつき(べき数)と構造の相関関係を明らかにするため、各粒子が接する粒子の個数分布(接触点数分布)を解析した結果、大きさの分布の指数aが3以下の条件では、等しい接触点数分布が現れることを発見し(図2)、極端に大きさがばらついた系では、個々の粒子の大きさの影響が弱まることで、むしろばらつきによらない共通した構造が現れることを明らかにしました。また、より隙間なく高密度に粒子を詰め込むことができるaの条件を見出しました(図3)。これにより、粒子集団に大きさのばらつきが特有の性質をもたらすことと、その条件が明らかになりました。
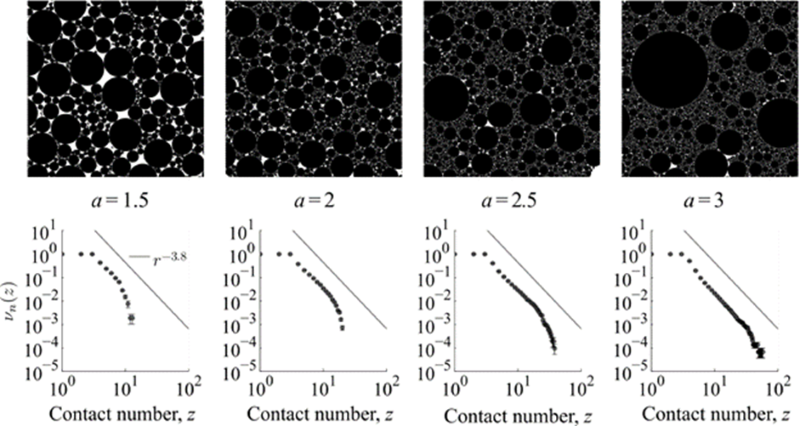
図2:シミュレーションから得られた、べき数aが異なるべき分布に従う粒子の配置(上)とそれぞれが示す接触点数の分布ν(z)(下)。ν(z)もべき分布となり、そのべき数は a < 3の条件では粒子半径のべき数aによらず、一定値となる。
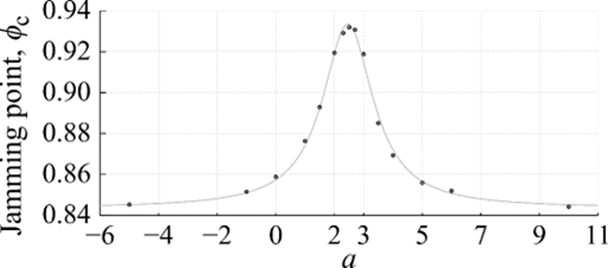
図3:ランダムに詰め込んだ粒子集団が固体のようにふるまいはじめる粒子密度ϕcと、粒子の大きさの分布を表すべき数aの関係。
社会的意義・今後の予定
系の大きい小さいによらず、岩石や生物細胞に含まれる分子のように、大きさのばらつきが極めて大きな粒子が密に詰め込まれた構造の理解へ貢献すると考えられます。今後は、こうした極端にばらついた粒子集団に対して、固さといった性質や、破壊や変形のしかたについても研究を進め、最終的には地震や細胞内でみられる現象の物理的解明へ繋げることを目指します。
謝辞
本研究は、科研費(JP21H05871, JP22H01188 [柳澤])、国立研究開発法人科学技術振興機構 創発研究支援事業(JPMJFR213Y [柳澤])の支援により実施されました。
論文情報
雑誌:「Physical Review Research」(オンライン版:2月10日掲載)
論文タイトル:Common Packing Patterns for Jammed Particles of Different Power Size Distributions
著者:Daisuke Shimamoto, Miho Yanagisawa*
DOI番号:10.1103/PhysRevResearch.5.L012014
用語説明
(注1)大きさがべき分布にしたがう粒子集団
粒子の半径rの分布が、r‐a(aは定数)のようなべき乗則に従うこと。