2026-02-13 スイス連邦工科大学ローザンヌ校(EPFL)
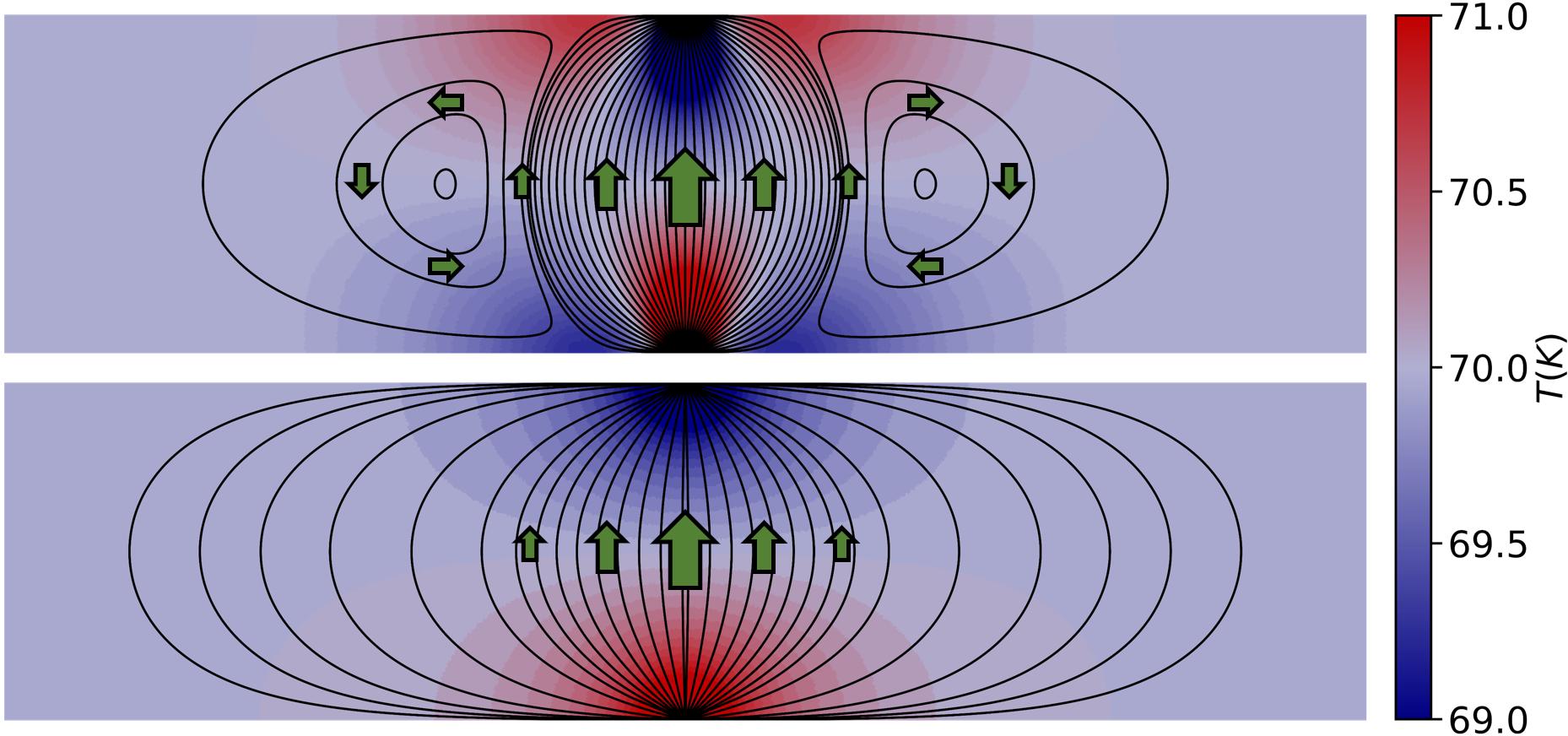
Vortex-induced heat backflow (top) in a simulated 2D graphite strip, compared with conventional heat flow (bottom). 2026 THEOS EPFL CC BY SA
<関連情報>
- https://actu.epfl.ch/news/when-heat-flows-like-water-2/
- https://journals.aps.org/prl/abstract/10.1103/g9dx-hjyn
- https://journals.aps.org/prx/abstract/10.1103/PhysRevX.10.011019
流体熱輸送における渦と逆流 Vortices and Backflow in Hydrodynamic Heat Transport
Enrico Di Lucente, Francesco Libbi, and Nicola Marzari
Physical Review Letters Published: 6 February, 2026
DOI: https://doi.org/10.1103/g9dx-hjyn
Abstract
Recent experiments have provided compelling and renewed interest in phonon hydrodynamics. At variance with ordinary diffusive heat transport, this regime is primarily governed by momentum-conserving phonon collisions. At the mesoscopic scale it can be described by the viscous heat equations (VHEs), that resemble the Navier-Stokes equations (NSEs) in the laminar regime. Here, we show that the VHEs can be separated and recast as modified biharmonic equations in the velocity potential and stream function—solvable analytically. These two can be merged into a complex potential defining the flow streamlines, and give rise to two distinct temperature contributions, ultimately related to thermal compressibility and vorticity. The irrotational and incompressible limits of the phonon VHEs are analyzed, showing how the latter mirror the NSEs for the electron fluid. This Letter also extends to the electron compressible regime that arises when drift velocities can be higher than plasmonic velocities. Finally, by examining thermal flow within a 2D graphite strip device, we explore the boundary conditions and transport coefficients needed to observe thermal vortices and negative thermal resistance, or heat backflow from cooler to warmer regions. This Letter provides analytical tools to design hydrodynamic phonon and electron flows, offering a foundational framework to understand and guide experiments on nonstandard transport, plasmonics, and collective excitations in microscale systems.
フーリエの法則の粘性熱方程式への一般化 Generalization of Fourier’s Law into Viscous Heat Equations
Michele Simoncelli, Nicola Marzari, and Andrea Cepellotti
Physical Review X Published: 28 January, 2020
DOI: https://doi.org/10.1103/PhysRevX.10.011019
Abstract
Heat conduction in dielectric crystals originates from the dynamics of atomic vibrations, whose evolution is well described by the linearized Boltzmann transport equation for the phonon populations. Recently, it was shown that thermal conductivity can be resolved exactly and in a closed form as a sum over relaxons, i.e., collective phonon excitations that are the eigenvectors of Boltzmann equation’s scattering matrix [A. Cepellotti and N. Marzari, Phys. Rev. X 6, 041013 (2016)]. Relaxons have a well-defined parity, and only odd relaxons contribute to the thermal conductivity. Here, we show that the complementary set of even relaxons determines another quantity—the thermal viscosity—that enters into the description of heat transport, and is especially relevant in the hydrodynamic regime, where dissipation of crystal momentum by umklapp scattering phases out. We also show how the thermal conductivity and viscosity parametrize two novel viscous heat equations—two coupled equations for the temperature and drift-velocity fields—which represent the thermal counterpart of the Navier-Stokes equations of hydrodynamics in the linear, laminar regime. These viscous heat equations are derived from a coarse graining of the linearized Boltzmann transport equation for phonons, and encompass both the limit of Fourier’s law and that of second sound, taking place, respectively, in the regime of strong or weak momentum dissipation. Last, we introduce the Fourier deviation number as a descriptor that captures the deviations from Fourier’s law due to hydrodynamic effects. We showcase these findings in a test case of a complex-shaped device made of graphite, obtaining a remarkable agreement with the recent experimental demonstration of hydrodynamic transport in this material, and also suggesting that hydrodynamic behavior can appear at room temperature in micrometer-sized diamond crystals. The present formulation rigorously generalizes Fourier’s heat equation, extending the reach of physical and computational models for heat conduction also to the hydrodynamic regime.



