2023-03-31 東京大学
発表のポイント
- ダンベル型分子の大規模シミュレーションによって、分子性液体がガラスとして固まる直前の運動メカニズムの全容を解明し、理論研究と実験研究の橋渡しとなる成果を得ました。
- 長時間と短時間で発生する運動がそれぞれ分子の回転と並進運動に起因することを明らかにし、これらの運動に明瞭な実空間的理解を与えました。理論的に重要なエネルギー地形描像に関しては、2段階の階層構造が上記の2つの過程を生み出すことを数値的に示し、提唱から25年以上経過した理論の正しさを証明しました。
- 本研究によって、実験的に観測されてきた運動の理論的な位置付けが明瞭になったことで、基礎理論の適用範囲を拡張する道が開け、将来的には現実世界に存在する多様なガラス的材料の制御や設計に貢献することが期待されます。
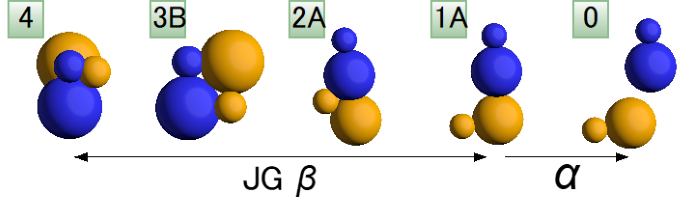
ダイマー粒子系の緩和の実空間描像
発表概要
ガラスは液体を急激に冷やすことで出来上がります。ガラスとして固まるガラス転移の直前では、液体分子は様々な時間スケールで複雑な運動をしています。これまでの数値研究は、液体の構成粒子を球や円盤などの等方的な形状をした粒子で単純化することが専らでした。しかし、分子性液体の実験で幅広く観察されてきたJohari-Goldstein β緩和（注1）と呼ばれる過程は等方粒子で捉えることができず、単純化の代償として当過程がどのような分子運動に相当するのか理解が進んでいませんでした。理論的には2段階の階層的なポテンシャルエネルギー地形（注2）による解釈が四半世紀以上前に提唱され、研究コミュニティに広く受け入れられてきましたが、同様の理由によりこの解釈の数値的な証拠を得ることは出来ませんでした。この状況は、現実の分子が示すガラス転移を説明する理論に対する、大きな不満となっていました。
東京大学大学院総合文化研究科の白石薫平大学院生、水野英如助教、池田昌司准教授の研究グループは、液体の構成粒子を異方的な形状にした系の大規模分子動力学シミュレーション（注3）を行いました。そして、上記に挙げた運動の実空間描像とエネルギー地形描像の双方の課題を解決しました。本研究によって実験的知見を説明する理論的立場が強固になったことで、ガラス転移研究における実験と理論の協同がこれまで以上に深化することが期待されます。
発表内容
我々の身の回りに溢れているガラスは、液体を冷やすことで生成されます。この冷却の最中、ガラスとして固まる直前には、液体は極めてドロドロとした状態になります。これを過冷却液体状態と呼びます。この状態で液体の分子がどのように運動するのかという問いは、ガラス転移という当分野の全体に関わる重大な問題です。
液体中で、分子は運動して時々刻々と位置を変えています。運動によって微視的な分子の空間的配置が変化することを「緩和」と呼びます。実験研究では、α緩和とJohari-Goldstein (JG) β緩和という2つの主要過程が存在することが、様々な分子性液体で確立されてきました。しかし、シミュレーションによる数値研究の注目は主に前者に限定されてきました。その理由は、過去のほとんどの研究が構成粒子を球や円盤などの等方的な形状に単純化して行われてきたからです。α緩和は等方粒子で捉えられる一方、JG β緩和は等方粒子のシミュレーションには現れないのです。JG β緩和をシミュレーションで捉えるには、ダイマー粒子のように構成粒子に「形」を持たせる必要があります。
ダイマー粒子とは、2つの原子がくっついた分子性液体のモデル粒子です（図1）。ダイマー粒子はJG β緩和を示す最も単純な分子性液体のモデルとして知られていました。しかし、等方粒子に比して過去に十分研究されてきたとは言えず、JG β緩和が分子のどのような微視的運動に起因するのかという基本的な論点でさえ、明らかではありませんでした。
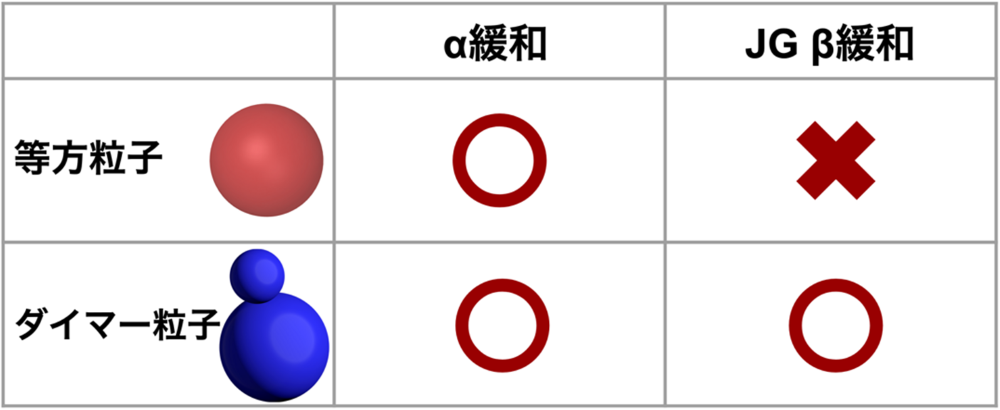
図1：等方粒子とダイマー粒子のシミュレーションが示す緩和過程の整理
他方、過冷却液体の緩和を説明する際に使われる理論的枠組みとして、ポテンシャルエネルギー地形描像があります。液体の粒子位置の情報が与えられたとき、ポテンシャルエネルギーの値が一つに定まります。ありとあらゆる粒子位置に対するポテンシャルエネルギーの値を、ポテンシャルエネルギー地形と呼びます。過冷却液体のエネルギー地形は図2のようにでこぼこな形状を取ると考えられており、過冷却液体の構造変化は、地形内の盆地状の構造間の遷移として捉えられます。そして、この描像では、過冷却液体がドロドロになる理由を、低温でエネルギー地形の盆地に系がはまって動けなくなるからだと説明します。
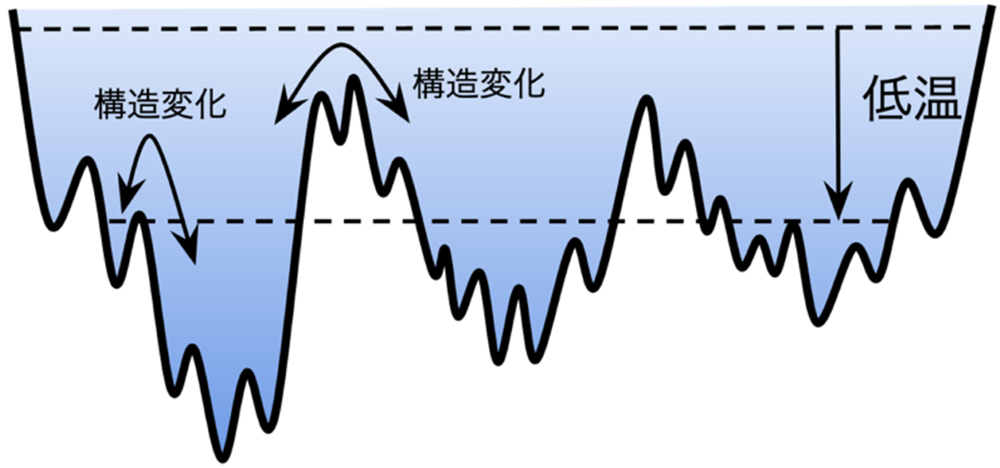
図2：ガラスのポテンシャルエネルギー地形の概念図
JG β緩和とα緩和という2つの過程が存在する分子性液体の場合、エネルギー地形は図3のような2段階の階層構造を持つと考えられてきました。この解釈では、小さい盆地が複数個集まって、より大域的な盆地を構成していると考えます。そして、JG β緩和が小さい盆地間の遷移、α緩和が大きな盆地間の遷移に対応するとされてきました。しかし、前述のように既存の研究のほとんどが等方粒子系を対象としてきたため、この2段階のエネルギー地形という解釈に対する数値的な証拠は与えられていませんでした。1995年の提唱以来、この解釈に対する証拠をシミュレーションで与えることは、分野の大きな目標となってきました。
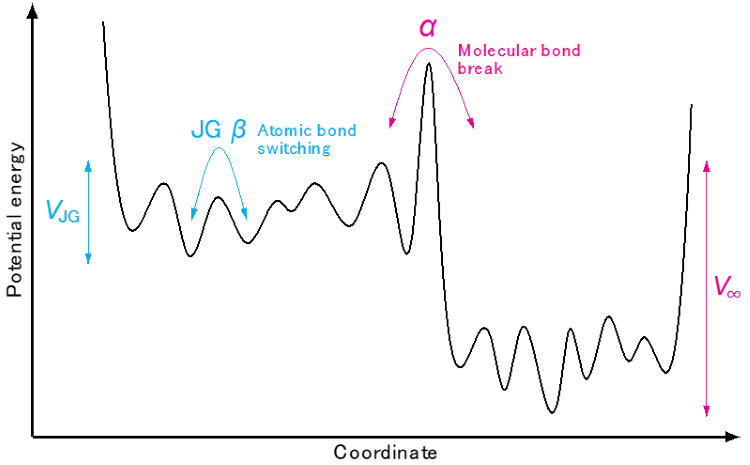
図3：本研究で調べた分子性液体のエネルギー地形の概念図
小さな盆地が複数集まって、大きな盆地を構成している。
本研究では、JG β緩和を示すダイマー粒子系の大規模な分子動力学シミュレーションを行いました。その結果、実空間とエネルギー地形の両面から、分子性液体の緩和過程に関する包括的な知見を得ました。
まず実空間では、分子を構成する原子同士がどのように接続しているかに着目して、分子同士の接続状態を分類しました。その結果、図4に示すような状態遷移に、99%以上の分子対が従うことが明らかになりました。この結果から、ダイマー系のJG β緩和とα緩和の実空間運動の詳細が分かります。JG β緩和は分子の回転運動によって、原子間接続が繋ぎ変わる運動です。他方、α緩和は分子の並進運動によって、最後に残った原子間接続、すなわち、それが担う分子間の接続が切断される運動です。
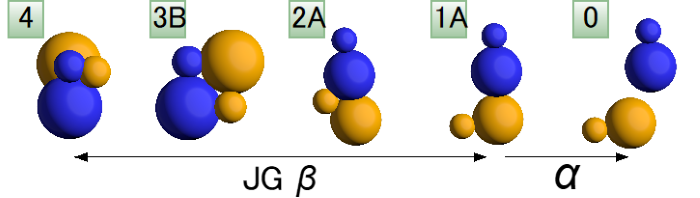
図4：ダイマー粒子系の緩和の実空間描像
そして、エネルギー地形の解析では、2段階のエネルギー地形を直接的に検証する研究を行いました。具体的には、各時刻で所在するエネルギー地形内の盆地でのエネルギーを計算し、それが時刻とともに初期値からどれだけ離れるかを定量化しました。すると、JG β緩和が発生する時間スケールではエネルギーが比較的狭い領域に限定されていることが分かりました（図3中のVJG）。そして、α緩和の時間スケールでは、より広い領域のエネルギーを取ることが分かりました（図3中のV∞）。これこそが、四半世紀以上前に理論的に提唱された2段階の階層的エネルギー地形を直接検出した、数値的証拠です。
以上、分子性過冷却液体の大規模シミュレーションによって、実験で報告されてきた緩和過程の全容を、実空間とエネルギー地形の両面から理解することに成功しました。これまでの理論・数値研究は、液体の粒子を等方的形状に理想化した状況に限定し、豊かな理解を構築してきました。これらの理解を、理想化が成り立たない現実世界の知見と接続するためには、本研究で用いたダイマー粒子のように複雑さを増した状況の研究を行い、既存の理解を拡張していくことが不可欠です。理論的側面以外からも、本研究で構築した分子性過冷却液体の緩和に対する理解は、金属材料から薬品に至るまで、身の回りに存在する多様なガラス的物質の制御や設計に向けた指針となります。
発表者
東京大学 大学院総合文化研究科 広域科学専攻
白石 薫平（博士課程）
水野 英如（助教）
池田 昌司（准教授）
論文情報
雑誌：Proceedings of the National Academy of Sciences of the United States of America
題名：Johari-Goldstein β relaxation in glassy dynamics originates from two-scale energy landscape
著者：Kumpei Shiraishi, Hideyuki Mizuno, Atsushi Ikeda
DOI：10.1073/pnas.2215153120
研究助成
本研究は、科研費 基盤研究(S)（課題番号：18H05225）、基盤研究(A)（課題番号：20H00128）、基盤研究(B)（課題番号：19H01812、20H01868）、基盤研究(C)（課題番号：22K03543）、特別研究員奨励費（課題番号：21J10021）、東京大学情報基盤センター若手・女性利用者推薦制度の支援を受けて実施されました。
用語説明
（注1）Johari-Goldstein β緩和
分子性過冷却液体の多くで観測される、比較的短時間で発生する分子運動のこと。緩和とは、運動によって微視的な分子の空間的配置が変化することを指す。どの時間で運動が発生するかを表す緩和スペクトルにおいて、Johari-Goldstein β緩和は独立したピークとして現れる。
（注2）エネルギー地形
過冷却液体の微視的な粒子の位置の全ての組み合わせに対するエネルギーの関数のこと。この描像は、ガラス転移の問題に限らず、タンパク質の構造変化、深層学習、化学反応など、科学や工学の幅広い問題で有用である。
（注3）分子動力学シミュレーション
微視的な粒子が従う運動法則をコンピューター上で直接計算し、粒子集団の運動を追跡する計算手法。
