2025-08-29 早稲田大学
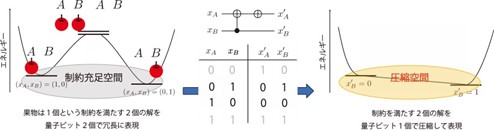
図1 組合せ最適化問題のもつ制約を量子計算機で圧縮して表現するための手法の概要。
図1の補足:図中央上は量子回路を表し、量子ゲート※3(左から制御NOTゲートとXゲート)を作用させることで、表(図中央下)で示した変換を実行する。
<関連情報>
制約付き組合せ最適化のための圧縮空間量子近似最適化アルゴリズム Compressed space quantum approximate optimization algorithm for constrained combinatorial optimization
Tatsuhiko Shirai; Nozomu Togawa
IEEE Transactions on Quantum Engineering Published:25 August 2025
DOI:https://doi.org/10.1109/TQE.2025.3602404
Abstract
Combinatorial optimization is a promising area for achieving quantum speedup. The quantum approximate optimization algorithm (QAOA) is designed to search for low-energy states of the Ising model, which correspond to near-optimal solutions of combinatorial optimization problems (COPs). However, effectively dealing with constraints of COPs remains a significant challenge. Existing methods, such as tailoring mixing operators, are typically limited to specific constraint types, like one-hot constraints. To address these limitations, we introduce a method for engineering a compressed space that represents the feasible solution space with fewer qubits than the original. Our approach includes a scalable technique for determining the unitary transformation between the compressed and original spaces on gate-based quantum computers. We then propose compressed space QAOA, which seeks near-optimal solutions within this reduced space, while utilizing the Ising model formulated in the original Hilbert space. Experimental results on a quantum simulator demonstrate the effectiveness of our method in solving various constrained COPs.



