2025-07-08 カリフォルニア大学サンタバーバラ校 (UCSB)
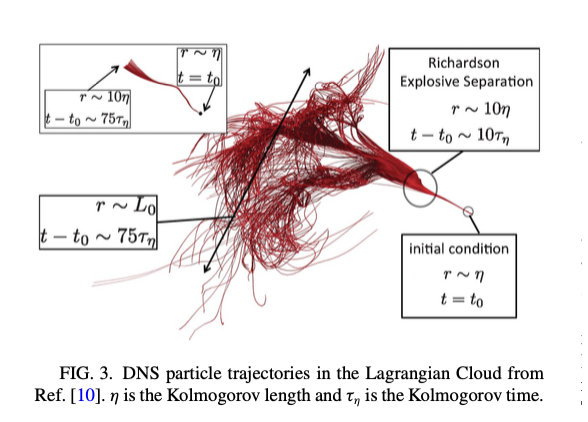
Photo Credit:Courtesy image
A simulation of Lagrangian turbulence, with a ballistic region on the right, superdiffusing into a Lagrangian region, followed by an Eulerian region and finally a region of “free eddies.”
<関連情報>
- https://news.ucsb.edu/2025/021949/new-mathematical-insights-lagrangian-turbulence
- https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.7.023225
ラグランジュ構造関数のスケーリング Scaling of Lagrangian structure functions
Björn Birnir and Luiza Angheluta
Physical Review Research Published: 3 June, 2025
DOI: https://doi.org/10.1103/PhysRevResearch.7.023225
Abstract
We use stochastic closure theory and generalized Green-Kubo relations to show that the velocity structure functions have two distinct scaling regimes connected by a passover. Initially, after a brief ballistic (Batchelor) scaling, the structure functions exhibit a Lagrangian scaling regime with no intermittency, and then pass over to a regime with Eulerian scaling, with intermittency. This transition time for the passover region is controlled by the second structure function, through a generalization of Green-Kubo-Obukhov relations. The ultimate time interval of decay seems to be controlled by the scaling of free eddies, analogous to the scaling in the buffer layer of boundary layer turbulence [B. Birnir, L. Angheluta, J. Kaminsky, and X. Chen, Spectral link of the Generalized Townsend-Perry constants in turbulent boundary layers, Phys. Rev. Res. 3, 043054 (2021)]. The dip observed in the log-derivatives of the structure function [L. Biferale, E. Bodenschatz, M. Cencini, A. S. Lanotte, N. T. Ouellette, F. Toschi, and H. Xu, Lagrangian structure functions in turbulence: A quantitative comparison between experiment and direct numerical simulation, Phys. Fluids 20, 065103 (2008)], with respect to the second structure function 2, is caused only by the time scales probed by 2. It seems better to take the log-derivative with respect to , instead of 2, to fully understand the different scaling regimes of Lagrangian turbulence.



