2024-07-01 サンディア国立研究所(SNL)
<関連情報>
- https://newsreleases.sandia.gov/quantum_advantage/
- https://arxiv.org/abs/2311.14123
- https://arxiv.org/abs/2106.04633
ストリーミングモデルにおける最大有向カットを近似する指数関数的量子空間の優位性 Exponential Quantum Space Advantage for Approximating Maximum Directed Cut in the Streaming Model
John Kallaugher, Ojas Parekh, Nadezhda Voronova
arXiv Submitted on 23 Nov 2023
DOI:https://doi.org/10.48550/arXiv.2311.14123
Abstract
While the search for quantum advantage typically focuses on speedups in execution time, quantum algorithms also offer the potential for advantage in space complexity. Previous work has shown such advantages for data stream problems, in which elements arrive and must be processed sequentially without random access, but these have been restricted to specially-constructed problems [Le Gall, SPAA `06] or polynomial advantage [Kallaugher, FOCS `21]. We show an exponential quantum space advantage for the maximum directed cut problem. This is the first known exponential quantum space advantage for any natural streaming problem. This also constitutes the first unconditional exponential quantum resource advantage for approximating a discrete optimization problem in any setting.
Our quantum streaming algorithm 0.4844-approximates the value of the largest directed cut in a graph stream with n vertices using polylog(n) space, while previous work by Chou, Golovnev, and Velusamy [FOCS ’20] implies that obtaining an approximation ratio better than 4/9≈0.4444 requires Ω(n−−√) space for any classical streaming algorithm. Our result is based on a recent O˜(n−−√) space classical streaming approach by Saxena, Singer, Sudan, and Velusamy [FOCS ’23], with an additional improvement in the approximation ratio due to recent work by Singer [APPROX ’23].
自然ストリーミング問題に対する量子的優位性 A Quantum Advantage for a Natural Streaming Problem
John Kallaugher
arXiv last revised 12 Nov 2021 (this version, v2)]
DOI:https://doi.org/10.48550/arXiv.2106.04633
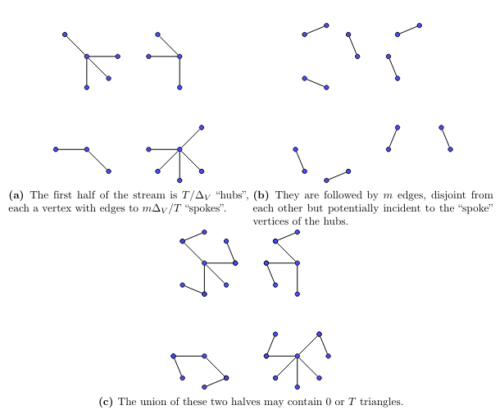
Abstract
Data streaming, in which a large dataset is received as a “stream” of updates, is an important model in the study of space-bounded computation. Starting with the work of Le Gall [SPAA `06], it has been known that quantum streaming algorithms can use asymptotically less space than their classical counterparts for certain problems. However, so far, all known examples of quantum advantages in streaming are for problems that are either specially constructed for that purpose, or require many streaming passes over the input.
We give a one-pass quantum streaming algorithm for one of the best studied problems in classical graph streaming – the triangle counting problem. Almost-tight parametrized upper and lower bounds are known for this problem in the classical setting; our algorithm uses polynomially less space in certain regions of the parameter space, resolving a question posed by Jain and Nayak in 2014 on achieving quantum advantages for natural streaming problems.



