2024-01-24 東京大学
発表のポイント
◆ 一次元的な古典系の確率的ダイナミクスに対して、緩和時間と緩和特性がトポロジカル指数で特徴づけられることを理論的に明らかにした。
◆ 従来はトポロジカル絶縁体など量子物質に対して適用されてきたトポロジーの概念を、古典力学的な確率的ダイナミクスに適用することでその緩和特性を明らかにした。
◆ 不純物などの乱れに左右されない熱力学デバイスの設計原理や、生体内の確率的ダイナミクスの特徴の解明などにつながると期待される。
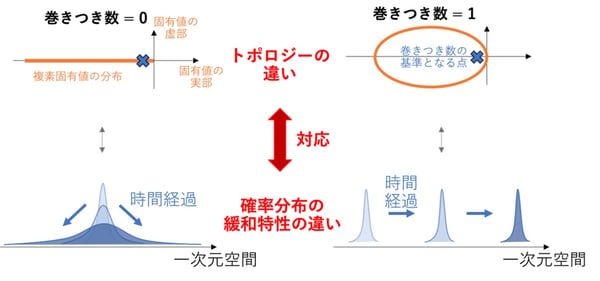
本研究におけるトポロジーと緩和現象の対応の概念図
概要
東京大学大学院工学系研究科物理工学専攻の澤田太郎大学院生、曽根和樹大学院生、沙川貴大教授、理化学研究所開拓研究本部の濱崎立資理研白眉研究チームリーダー(理化学研究所 数理創造プログラム 上級研究員)、東京大学大学院理学系研究科物理学専攻の蘆田祐人准教授らの研究グループは、一次元的に動く古典系の確率的ダイナミクス(注1)に対して、緩和時間(注2)と緩和特性がトポロジカル指数(注3)と対応することを理論的に明らかにしました。これらの関係は、本研究で導入したトポロジカル指数である「巻きつき数(注4)」と、確率的ダイナミクスとの深いつながりを示しています。本研究結果は、既存の非エルミート系(注5)の研究では理解されていなかった、古典系の確率的ダイナミクスに特有のトポロジー(注6)の性質を初めて明らかにしたものであり、不純物などに起因する乱れに左右されない熱力学デバイスの設計原理や、生体内の確率的ダイナミクスの特徴の解明などにつながると期待されます。
発表内容
【研究の背景】
散逸(注7)の少ないデバイスを設計するために、トポロジーという数理的概念の利用が注目を集めています。最も基本的な例であるトポロジカル絶縁体では、トポロジカル指数の値に対応して、不純物などに起因する乱れに対しても安定して存在する電流が系の端を伝って流れうることが知られています。また、近年は散逸のある非エルミート系にもトポロジーの概念が拡張され、活発に研究が行われています。しかし、このようなトポロジーと物性の関係を調べる研究は、主に量子力学の効果が主要な系(量子系)を中心として行われており、古典力学で記述される系(古典系)においては未開拓でした。特に確率的ダイナミクスに従う古典系は熱力学的デバイスから細胞内の分子機械まで幅広く存在するため、新たな理論的枠組みに基づく理解が望まれていました。
【研究内容】
本研究では、一次元的な確率的ダイナミクスに従う古典系のトポロジカル指数として、確率遷移行列(注8)の複素固有値の巻きつき数を導入し、それが系の緩和時間と緩和特性と対応することを明らかにしました。緩和時間については、系が大きくなるにつれて発散することを理論的に示した上で、さらに巻きつき数が緩和時間の発散の速さと対応することを発見しました。また、緩和特性については、過渡領域におけるカットオフ現象(注9)の存在が、巻きつき数の値から予測できることを明らかにしました。緩和現象とトポロジーの対応は、広汎なモデルに対する数値計算によって確認されました(図1参照)。
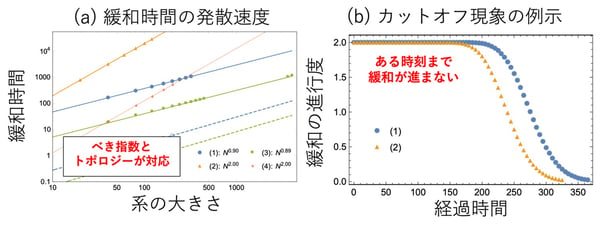
図1:本研究でトポロジーとの対応が示唆された緩和現象の数値的な検証
(a)緩和時間の系の大きさへのべき的な依存性。それぞれの巻きつき数は(1)(3)が非ゼロであり、(2)(4)がゼロとなるように設定した。非ゼロかどうかに対応してべき指数が決まっている。(b)トポロジカル指数から存在が予測されるカットオフ現象の例示。(1)(2)ではともに非ゼロな巻きつき数をもつパラメータに設定した。これらの結果はパラメータの値そのものではなくトポロジカル指数が緩和特性を決定することを意味している。
なお、本研究結果は既存の非エルミート系のトポロジー理論のみからは導出されないものであり、確率的ダイナミクス特有の性質を組み合わせることで初めて理論的に導出されます。このことは、古典系の確率的ダイナミクスに特有のトポロジー的性質があることを本研究が初めて明らかにしたことを意味しています。
【研究の意義、今後の展望】
本研究結果は、散逸の少ないデバイスの設計に役立つトポロジーの概念を確率過程に適用し、緩和特性との対応を示したことで、外的な乱れに左右されない熱力学デバイスの設計原理につながることが期待されます。また、細胞内の分子機械などのダイナミクスは古典確率過程で記述されるため、生体システムの頑健性(注10)の理解にも役立つことが期待されます。さらに、確率的なダイナミクスに従う古典系に対するトポロジーの有用性を示したことで、トポロジカル物理の地平を広げたという基礎物理としての意義も持ちます。
発表者・研究者等情報
東京大学
大学院工学系研究科物理工学専攻
澤田 太郎 博士課程
曽根 和樹 博士課程
沙川 貴大 教授
兼:附属量子相エレクトロニクス研究センター
大学院理学系研究科附属知の物理学研究センター
蘆田 祐人 准教授
兼:物理学専攻
理化学研究所開拓研究本部非平衡量子統計力学理研白眉研究チーム
濱崎 立資 理研白眉研究チームリーダー
論文情報
雑誌名:Physical Review Letters
題 名:Role of Topology in Relaxation of One-Dimensional Stochastic Processes
著者名:Taro Sawada*, Kazuki Sone, Ryusuke Hamazaki, Yuto Ashida, Takahiro Sagawa
DOI:10.1103/PhysRevLett.132.046602
研究助成
本研究は、JST ERATO「沙川情報エネルギー変換プロジェクト」(課題番号:JPMJER2302)、JST ERATO 特定領域調査「情報エネルギー変換」(課題番号:JPMJER2204)、JST 創発的研究支援事業「量子多体物理と量子光学の融合で探る強結合開放系の物理」(課題番号:JPMJFR222U)、JSPS科学研究費助成事業新学術領域(研究領域提案型)「情報物理学でひもとく生命の秩序と設計原理」の計画研究班「情報熱力学による生体情報処理の理論研究」(課題番号:JP19H05796)、JSPS科学研究費助成事業若手研究(課題番号:JP21K13859)、JSPS特別研究員奨励費「アクティブマターにおけるトポロジカル現象の研究」(課題番号:21J20199)、東京大学統合物質・情報国際卓越大学院(MERIT-WINGS)、東京大学Beyond AI研究推進機構の支援により実施されました。
用語解説
(注1)確率的ダイナミクス
次の時刻でのシステムの状態が確率的に決まるような運動のことを、ここでは確率的ダイナミクスと呼んでいます。数学的には確率過程と呼ばれるものです。
(注2)緩和時間
時間的に変化しない状態を定常状態と呼びます。ダイナミクスによって、系が定常状態に十分近づいたとみなせるまでにかかる時間を緩和時間と呼びます。
(注3)トポロジカル指数
トポロジカル指数とは、後述するトポロジーの観点で図形を分類したときに、その分類を特徴づける量です。例えばボールとドーナツの例では、穴の数がトポロジカル指数となります。物理学では、物理系のエネルギー構造を決めるハミルトニアンなどに対してトポロジカル指数を定義します。
(注4)巻きつき数
平面内にある曲線が、特定の基準点の周りをどれだけ回ったかを数える数学的な量です。基準点を横切るような変形をしない限り、曲線の回転数は変化しないので、これはトポロジカル指数の例になっています。
(注5)非エルミート系
従来の量子力学においては、エネルギーが実数であることに対応してハミルトニアンがエルミート行列であることを仮定していますが、それを非エルミート行列にも拡張したのが非エルミート系の物理です。これは散逸のある状況を記述することが知られており、実際の実験状況でノイズの効果などを考慮できるという利点から近年盛んに研究されています。
(注6)トポロジー
図形に対して連続的な変形のみを許した際に変わらない性質を調べる数学です。そのような性質を基に、図形を分類する指標となるのが先述のトポロジカル指数です。例えば、穴の空いていないボールとドーナツは穴の数という性質が異なるので、穴の数を見るだけで図形が異なることがわかります。
(注7)散逸
注目しているシステムのエネルギーなどが外界へと失われることを、散逸があると言います。
(注8)確率遷移行列
確率的ダイナミクスを時間に関する微分方程式の形で書いたときに、状態間の遷移確率を与える行列です。この行列の固有値問題を解くことで、緩和時間や定常状態についての情報が得られます。
(注9)カットオフ現象
確率的ダイナミクスによって系が時間変化する際、過渡領域での緩和の進行度を考えると、一定の割合で緩和が進まない場合があります。そのような状況のうち、ある時刻までは全く緩和が進まず、その後急に緩和が進行するような振る舞いのことを、カットオフ現象とよびます。数学ではトランプのシャッフル回数による混ざり具合を例として、古くから知られている現象です。
(注10)頑健
ある現象が頑健であるとは、その性質が不純物に起因する乱れなどの下でも残り続けることを言います。たとえば、量子ホール効果は不純物の存在に対して頑健であることが知られており、その起源はトポロジーであると考えられています。
プレスリリース本文:PDFファイル
Physical Review Letters:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.046602