2025-08-06 韓国基礎科学研究院(IBS)
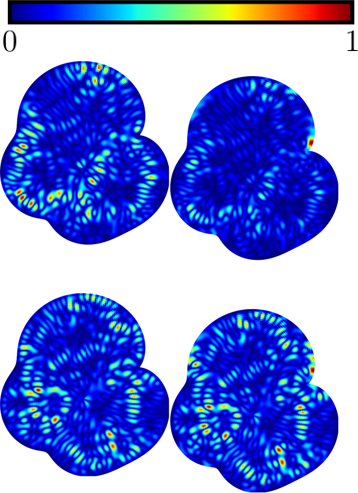
Figure 1. The left part shows the outgoing current using the eigenstates computed with BIM, the right one those computed with CMM. For the BIM, the outgoing current vanishes along the boundary as required by the BC, whereas for the CMM, it clearly deviates from zero.
<関連情報>
- https://www.ibs.re.kr/cop/bbs/BBSMSTR_000000000738/selectBoardArticle.do?nttId=26040&pageIndex=1&searchCnd=&searchWrd=
- https://journals.aps.org/prl/abstract/10.1103/vj94-kc98
相対論的量子ビリヤードにおける等角写像法の失敗 Failure of the Conformal-Map Method for Relativistic Quantum Billiards
Barbara Dietz
Physical Review Letters Published: 15 July, 2025
DOI: https://doi.org/10.1103/vj94-kc98
Abstract
In H. Xu et al. [Phys. Rev. Lett. 110, 064102 (2013)], a numerical method is introduced—an extension of the conformal-map method of Robnik [J. Phys. A 17, 1049 (1984)] for nonrelativistic quantum billiards—for the quantization of relativistic neutrino billiards consisting of a massless noninteracting spin-1/2 particle confined to a two-dimensional domain. We demonstrate in this Letter that this method does not provide solutions of the associated Weyl (Dirac) equation, nor does it fulfill the boundary conditions imposed on the spinor eigenfunctions to ensure confinement of the particle to the domain of the billiard. We review in detail the wave equation, boundary conditions, and quantization of neutrino billiards and derivation of relevant equations to make the proof comprehensible for the general reader. Our results are corroborated with numerical ones for nonrelativistic and relativistic quantum billiards whose shapes depend on a parameter, which allows the study of the properties of their eigenstates as the classical dynamics experiences a transition from regular to chaotic dynamics.



