多座配位子内の二面角変化に基づく構成成分数の多い自己集合体の形成～大きな構造体形成の一般原理～

2024-09-09 東京大学

発表のポイント

• 多座配位子内の二面角を大きくすることで、構成成分数の多い一義集合体を形成することが明らかになりました。
• 速度論支配および熱力学支配による自己集合において、多座配位子の二面角を大きくすると、なぜ大きな構造体が形成するのかという形成原理を構造体の幾何学に着目し解明しました。
• 自然界に存在するウイルスの殻構造などに見られる大きな自己集合体形成に対する理解、人工的な自己集合系における大きな構造体の設計指針への貢献が期待されます。

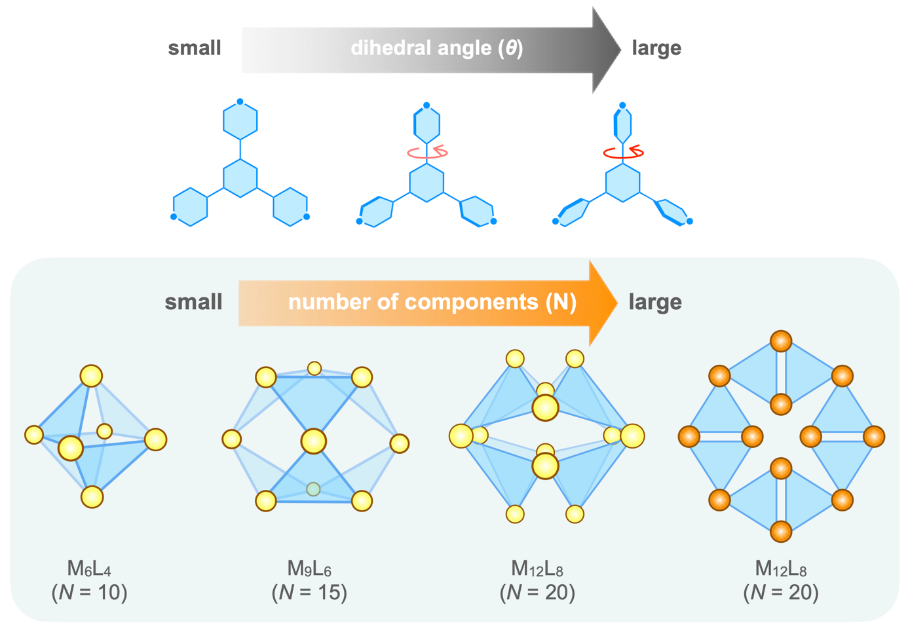
多座配位子内の二面角変化に伴う成分数の多い構造体の形成

発表内容

東京大学大学院総合文化研究科の平岡秀一教授、京都大学大学院工学研究科の佐藤啓文教授、および名古屋大学大学院情報学研究科の東雅大教授らによる研究グループは、多座配位子内の二面角が異なる三座配位子とcis-保護されたPd錯体から自己集合を行い、二面角を変化させることで速度論支配（注1）および熱力学支配（注2）により、それぞれ構成成分数の多い自己集合体が形成することを明らかにしました。また、幾何学解析（注3）という独自に開発した方法を用いて大きな構造体の形成原理を解明しました。

〈研究の背景〉
分子自己集合は、小さな構成成分が集まり一義構造体を形成する現象です。構成要素を結ぶ相互作用には可逆性があるために、多くの自己集合は熱力学平衡状態（注4）に達し、生成物はマクスウェル・ボルツマン分布（注5）に従い決定されます。自己集合体を形成すると構成成分の自由度が束縛されるため、自己集合はエントロピー（注6）的に不利な現象で、構成成分数が増加するにつれて、エントロピーの不利分が大きくなります。したがって、構成成分間の相互作用から生じるエンタルピー（注7）による利得が同じ場合、構成成分数の多い構造体の形成は困難です。一方、自然界にはウイルスの殻構造（カプシド）（注8）やフェリチン（注9）のような多数の構成成分からなる集合体が存在するため、エントロピーの不利を乗り越えて大きな構造体を形成する一般原理が存在するはずですが、その詳細は明らかにされていません。

人工系の自己集合の一例として、金属イオンと多座配位子の間に形成される配位結合を利用した配位自己集合があります。配位自己集合は、金属イオンの配位構造と多座配位子の配位方向の組み合わせにより多種多様な幾何構造を形成できるデザイン性の高い手法で、同一の配位方向をもつ金属イオンと多座配位子からは同一の構造体を形成すると考えられてきました。

〈研究の内容〉
本研究では、中心芳香環とそれに結合した3つの4-ピリジン環の二面角が異なる三座配位子を用いてcis位の保護基としてTMEDA(N,N,N’,N’-teramethylethylendiamine)を有するPd錯体(=M)との自己集合を実施しました。二面角(θ)が0°のトリアジン中心をもつ三座配位子(1)では[M₆1₄]¹²⁺切頂四面体構造体を形成するのに対し（図1a）、θが36.5°のベンゼン中心をもつ三座配位子(2)では、速度論的生成物（注10）として[M₉2₆]¹⁸⁺切頂三角錐三角柱プリズムが96%の収率で得られ、一方、熱力学的生成物（注11）として[M₁₂2₈]²⁴⁺切頂二十面体構造が定量的に生成し、配位方向を維持したまま二面角を大きくすることで構成成分数の多い構造体が形成することを見出しました（図1b）。配位子の二面角変化によりなぜ構成成分数の異なる構造体が形成したのかを調べるため、構造体におけるPdと配位子の連結構造および部分環構造の幾何学に着目しました。

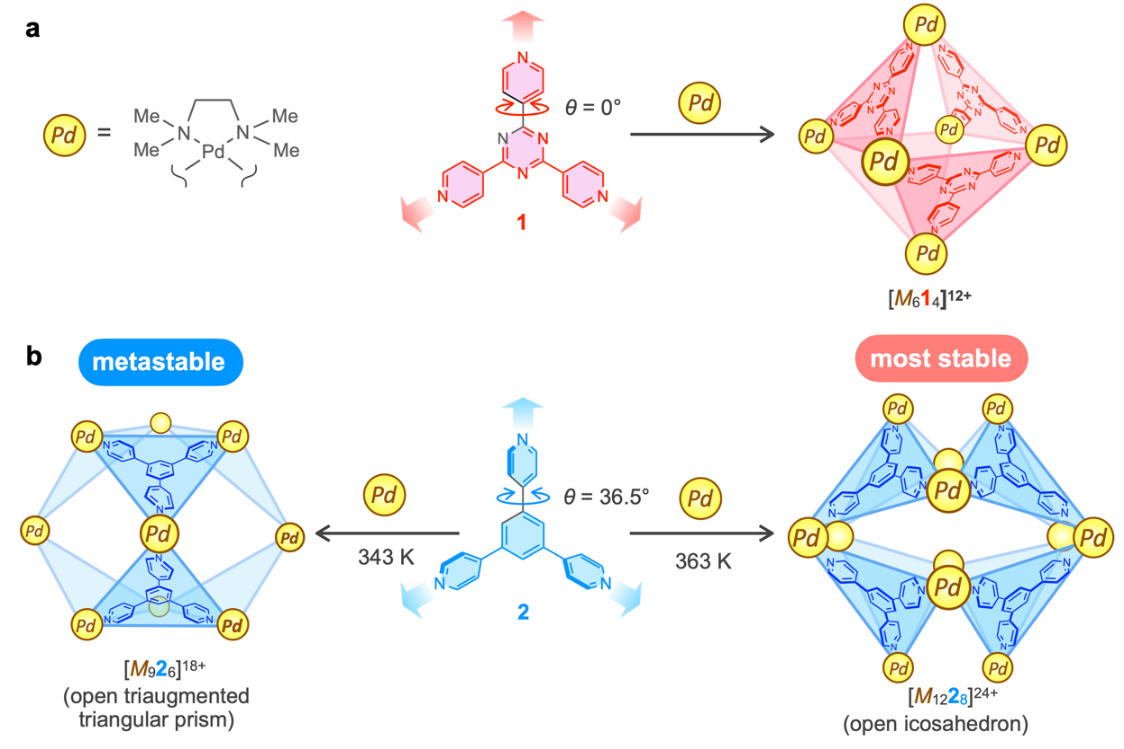
図1：二面角の異なる三座配位子とcis保護されたPd錯体(M)から形成される自己集合体(a) 配位子1を用いた[M₆1₄]¹²⁺切頂四面体構造の形成。(b) 配位子2を用いた[M₉2₆]¹⁸⁺頂三角錐三角柱プリズムおよび[M₁₂2₈]²⁴⁺切頂二十面体構造の形成。[M₉2₆]¹⁸⁺構造体は速度論支配、[M₁₂2₈]²⁴⁺構造体は熱力学支配によって得られた。[M₉2₆]¹⁸⁺は343 K, 2日で収率96%, [M₉2₆]¹⁸⁺はNO_3-存在下363 K, 5日で定量的に生成する。

Pdと配位子の連結部分ではPdのcis保護基と結合する三座配位子の立体的要因により三座配位子の立体配置がある程度固定され、それにより配位方向が決まることがわかりました。さらに配位方向は直接結合していない別の三座配位子にもPdを介して構造の規制が反映されることから、我々は遠隔の幾何学的相関 (Remote Geometric Communication)（注12）と呼んでいます。実際にθ= 0°のトリアジン中心配位子1とベンゼン中心配位子2における[ML₂]²⁺に着目すると[M2₂]²⁺の方がピリジン環の向きがより広く向いており、大きな構造体形成の鍵となることを見出しました（図2）。

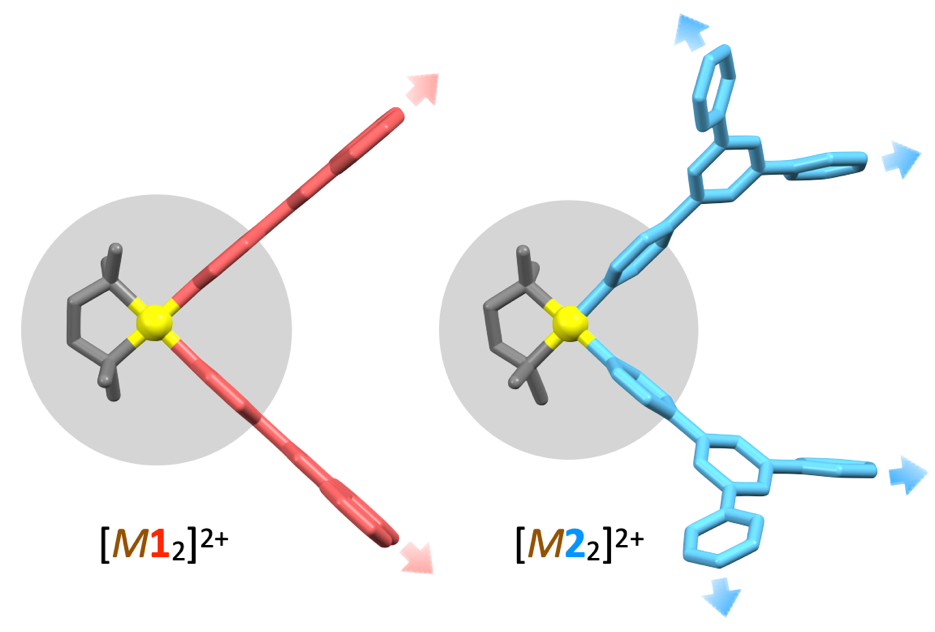
図2：Pdを介した2つの三座配位子(1および2)の配位方向の概念図Pd上の保護基により三座配位子の立体配置が制限され、配位方向が固定される。片方の三座配位子の配置がPdを介して直接は結合していない、別の配位子にも反映される。これを遠隔の幾何学的相関 (Remote Geometric Communication) と呼び配位子間の幾何情報の伝播も大きな構造体を形成する上で重要であることがわかった。黄色はPd, 灰色は炭素原子、赤は配位子1、水色は配位子2を表す。

一方、環構造に着目すると、[M₆1₄]¹²⁺および[M₉2₆]¹⁸⁺は三員環および四員環、[M₁₂2₈]²⁴⁺は四員環構造を内部に有しています（図3a）。そこで我々は独自に開発した幾何学解析を用いて配位子の二面角(θ)と環状構造の歪みをRing Strain per Unit (RSU)（注13）の尺度を用いて評価しました。RSUは金属(M)-配位子(L)-金属(M)-配位子(L) ···の順で構成されます。MnLnの環構造において、MとLの結合をn通りの箇所で切断後に歪みを解消した構造において、両末端のMの間の距離を算出し、これらの平均をnで割った値がRSUで、これが小さいほどMnLn環構造の歪みが小さいと言えます（図3b）。[M₁₂2₈]²⁴⁺の結晶構造中の二面角θ = 38°におけるRSUは0.010と部分環構造の歪みがとても小さいことが明らかになりました（図3c）。一方、[M₉2₆]¹⁸⁺の安定構造における三員環および四員環内のθの平均値(それぞれ30°および34°)におけるRSUは0.220および0.470と[M₁₂2₈]²⁴⁺と比べ歪みが大きく（図3d）、[M₁₂2₈]²⁴⁺が熱力学的安定種、[M₉2₆]¹⁸⁺が準安定種となった理由が、部分環構造の幾何学的な歪みに由来することを明らかにしました。

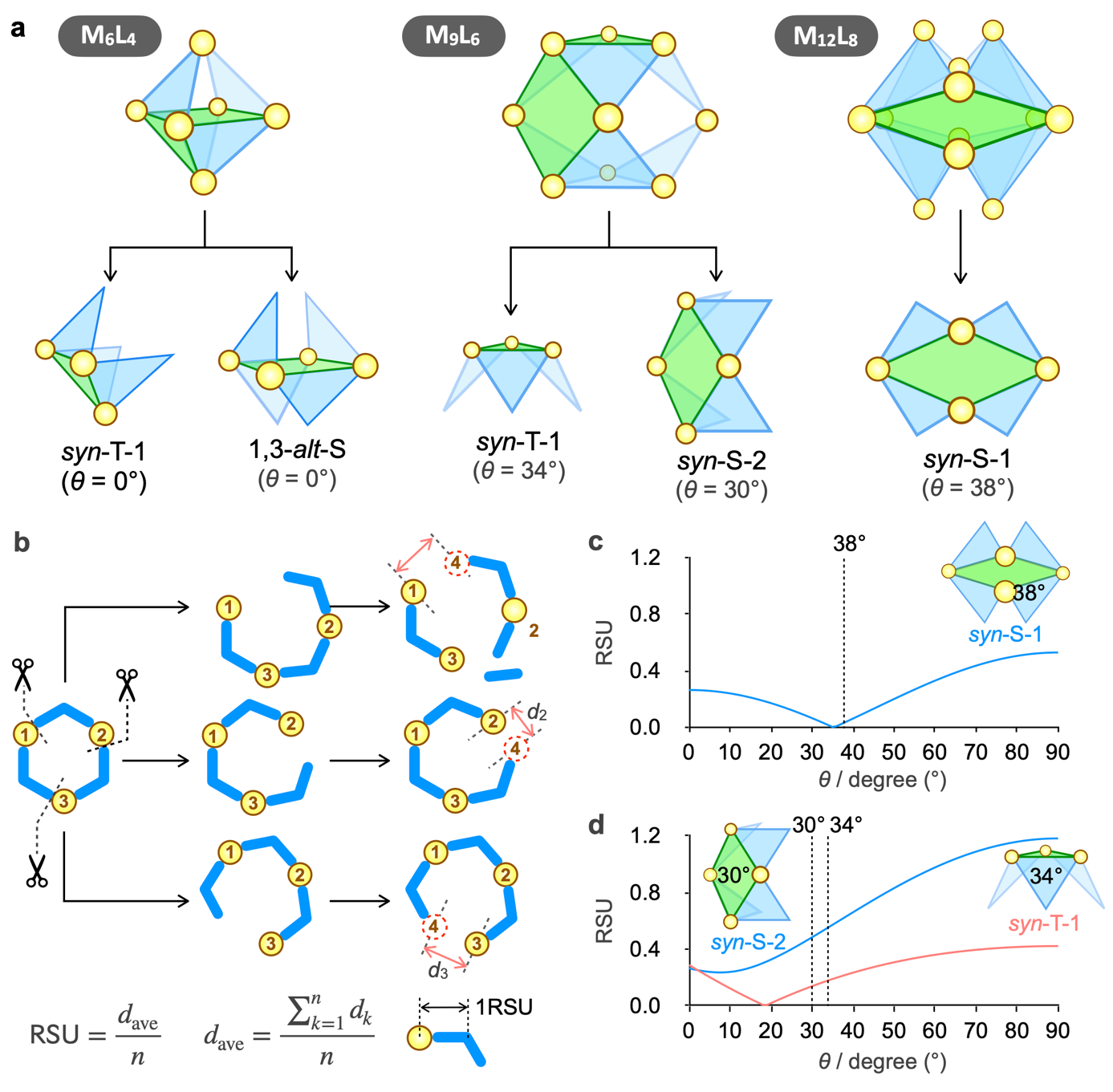
図3：環状構造の幾何学解析(a) [M₆L₄]¹²⁺, [M₉L₆]¹⁸⁺および [M₁₂L₈]²⁴⁺構造体の部分環構造。[M₆L₄]¹²⁺は三員環と四員環、[M₉L₆]¹⁸⁺は三員環と四員環、[M₁₂L₈]²⁴⁺は四員環を有する。(b) 環状構造の歪みの評価方法とRSUの定義。1つの金属と1つの配位子の中心を結んだ距離を1 RSUとする。環状構造は、M-L-M-L··の順に構成される。MnLn環状構造では、MとLの結合をn通りの箇所で切断後に歪みを解消した後、それぞれの箇所で切断した末端のMの間の距離を算出する。この平均をnで割ることでRSUを算出し、RSUの値が小さいほど歪みが小さいと評価する。二面角(θ)の変化に対する(c) [M₁₂L₈]²⁴⁺および (d) [M₉L₆]¹⁸⁺構造体の部分環構造における歪み（RSU）との関係。θ＝38°は[M₁₂L₈]²⁴⁺の結晶構造における四員環構造の平均値。[M₉L₆]¹⁸⁺ではDFT計算によリ得られた最適化構造を用い、θ＝ 34°および30°は最適化構造の三員環（ピンク）および四員環（水色）構造のθの平均値である。

〈今後の展望〉
本研究では構成要素間の幾何学的なデザインにより大きな自己集合体の形成が可能であることを示しました。自然界において、なぜ大きな自己集合体の形成が可能なのかという一般原理を明らかにするためには、構成成分間の相互作用の本質をより深く理解する必要があります。単純な人工システムは、複雑な生命システムの根底にある本質を抽象化する優れたモデルとなり得ます。本モデル系から、構成要素自体の合理的な設計を超えて、構成要素間の幾何学情報の伝播の重要性が明らかとなり、大きな自己集合体を設計する新しい指針を与えることができました。

また、配位子2を用いた自己集合では、準安定な[M₉2₆]¹⁸⁺が96%の収率で生成しました。これは速度論支配により単一成分を形成できることを示しています。自然界では、速度論的制御が分子自己集合に関与することがありますが、速度論的制御の理解は速度論トラップ（注14）を超えたものではありません。速度論的制御の利点は、準安定な集合体にもアクセスできることであり、これにより分子自己集合の可能性が広がります。[M₉2₆]¹⁸⁺構造体への自己集合経路を理解することで、分子自己集合における速度論的制御の一般原理を解明し、速度論支配の自己集合を合理的に設計できるようになると期待されます。

発表者・研究者等情報

東京大学大学院総合文化研究科広域科学専攻相関基礎科学系
平岡　秀一　教授
阿部　司　助教
竹内　啓介　修士課程

京都大学大学院工学研究科分子工学専攻
佐藤　啓文　教授

名古屋大学大学院情報学研究科複雑系科学専攻
東　雅大　教授

論文情報

雑誌名：Nature Communications （オンライン版）
題名：Rational design of metal-organic cages to increase the number of components via dihedral angle control
著者名：Tsukasa Abe, Keisuke Takeuchi, Masahiro Higashi, Hirofumi Sato, and Shuichi Hiraoka*
DOI：10.1038/s41467-024-50972-z
URL：https://doi.org/10.1038/s41467-024-50972-z

研究助成

本研究は、科研費「速度論支配下で働く配位自己集合の原理の解明（課題番号：21K18974）」、「速度論支配による多成分自己集合性錯体の創成（課題番号：23H01970）」、旭硝子財団の支援により実施されました。

用語説明

（注1）速度論支配
AとBの間で不可逆な共有結合を形成してCを与える化学反応では、反応の進みやすさは遷移状態と始原系のエネルギー差、すなわち活性化エネルギーで支配されること。

（注2）熱力学支配
AとBの間で可逆な化学結合を形成してCを与える化学反応では、Cが生成するかは、AとBのエネルギーの和とCとの自由エネルギー差で支配されること。

（注3）幾何学解析
分子の軌道（電子密度）は考慮せず、原子間の距離や角度など純粋な幾何学パラメータのみを用いて評価する解析手法のこと。

（注4）熱力学平衡状態
可逆反応において、正反応と逆反応が同じ速度で進行している状態のこと。反応系全体では、見かけ上何の変化も起こっていないように見える。

（注5）マクスウェル・ボルツマン分布
理想気体の熱力学平衡状態における気体分子の確率分布のこと。

（注6）エントロピー
示量性の物理量。熱力学において現象の不可逆性を表す量のこと。統計力学では分子・原子の運動の秩序の度合いを表す量のこと。

（注7）エンタルピー
示量性の物理量。物体が内部に蓄えている総エネルギー量のこと。

（注8）ウイルスの殻構造（カプシド）
ウィルスゲノムを取り囲むタンパク質の殻のこと。数百ものタンパク質からなる自己集合体であり、代表的なものは正二十面体を形成する。

（注9）フェリチン
24個のサブユニットからなる球状タンパク質で、生体内において鉄と結合し保存および放出を行うタンパク質のこと。

（注10）速度論的生成物
速度論支配における自己集合で得られる生成物のこと。生成物は自己集合の経路に依存し、準安定種であることが多い。

（注11）熱力学的生成物
熱力学支配における自己集合で得られる生成物のこと。生成物は自己集合の経路に依存せず、主生成物は熱力学的に最安定種である。

（注12）Remote Geometric Communication
配位結合が形成されているPdと配位子の間において、Pdのcis保護基と三座配位子の立体障害により三座配位子の立体配置が固定される時、別の三座配位子にも配位方向が伝播される。配位子同士は直接結合しておらずPdを介して遠隔で構造情報を伝播しているので遠隔の幾何学的相関 (Remote Geometric Communication) と呼ぶ。

（注13）Ring Strain per Unit (RSU)
環状構造の歪みを評価するために導入した尺度のこと。単位は距離。1つの金属(M)とそれに隣接する1つの配位子(L)の中心を結んだ距離を1RSUとする。MnLn環状構造は、M-L-M-Lの順で構成され、MとLの結合をn通りの箇所で切断後に歪みを解消した後、それぞれの箇所で切断した両末端のMの間の距離を算出する。この平均をnで割ることでRSUを算出し、値が小さいほど歪みが小さいことを示す。

（注14）速度論トラップ
大域的な反応の途上にエネルギー障壁が高い素反応が存在する場合、反応ネットワークが可逆であっても化学平衡に至らない場合があり、そのときに得られる化学種を速度論トラップとよぶ。